ответ:
) а) f(x) = 1/5x5 - x3 + 4.
f'(х) = 1/5 * 5 * х4 – 3х² = х4 – 3х².
б) f(x) = (3x – 1)/x3.
производная произведения: (f * g)' = f' * g + f * g'.
f'(х) = (3x – 1)' * x3 + (3x – 1) * (x3)' = 3 * x3 + (3x – 1) * 3x² = 3x3 + 9x3 – 3x² = 12x3 – 3x².
в) f(x) = 1/(2cosx).
производная дроби: (f/g)' = (f' * g - f * g')/g^2.
f'(х) = (1' * 2cosx - 1* (2cosx)')/( 2cosx)^2 = (0 - 1* (-2sinx))/2cos²x = sinx/cos²x.
2) а) f(x) = xsinx.
f'(х) = х' * sinx + х * (sinx)' = sinx + хcosx.
x = п/2; f'(п/2) = sinп/2 + п/2cosп/2 = 1 + п/2 * 0 = 1.
б) f(x) = (2x - 3)6.
f'(х) = 6(2х – 3)5 * (2х – 3)' = 6(2х – 3)5 * 2 = 12(2х – 3)5.
х = 1; f'(1) = 12(2 * 1 – 3)5 = 12 * (-1)5 = -12.
3) а) f(x) = 2sinx – x.
f'(х) = 2cosx – 1.
f'(х) = 0; 2cosx – 1 = 0.
2cosx = 1.
cosx = ½.
х =±п/3 + 2пn, n – целое число.
b) f(x) = x5 + 20x².
f'(х) = 5х4 + 20х.
f'(х) = 0; 5х4 + 20х = 0.
х(5х3 + 2) = 0.
отсюда х = 0.
или 5х3 + 2 = 0; 5х3 = -2; х3 = -2/5; х = 3√(-2/5).
объяснение:
Стандартные решения через дискриминант уже написаны, можно по ним свериться. Предложу "быстрые", но которые не всегда срабатывают.
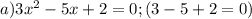- видно, что сумма коэффициентов в этом квадратном уравнении равна 0. Корни находятся быстро и безболезненно.
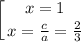
ответ: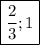 
б) тут действительно проще всего выделить полный квадрат. С опытом приходит их видение.
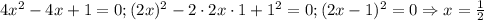
ответ: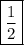 
в)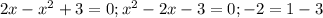 
Здесь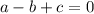 
или проще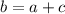 
В этом случае
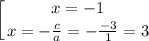
ответ: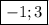 
P.S. как видим, ни разу не был вычислен дискриминант. И примеров таких уравнений довольно много, в том числе и на экзаменах. Поэтому советую запомнить эти частные случаи и тренироваться побольше.
7x=2-9
7x=-7
x=-1
x^2 из корня выходит как x