М тут все придельно легко
итак в третьем задании решишь немного по иному не пропорцией,там как в первом только в третьем ты должен(на) Либо у большего числителя разделить меньший числитель и в итоге какое число получиться тоже число и умножить на известный знаменатель .Тоже самое со знаменателем,только там делить и умножать числители. Рассмотрим пример 3/7 ＝x/28 ,x-неизвестный числитель.Значит нам нужно искать число на которое мы будем умножать из знаменателей, там у нас 28 и 7;;;28:7＝4 .Мы нашли число знаменателя во сколько раз один больше другого. и умнржаем изв числитель на это число 3＊4＝12, и того ×＝12. Надеюсь я разъяснил все внятно)Удачи на контрольной.
Незнаю как ты там звания зарабатываешь и про корни решаешь 7 класс там даже в 10- тичных дробях ,если ты еще не можешь обыкновенные решать.В некоторых случаях ответ в сложных примерах не получается только в десятичных , а если то на то и получаеться но в очень длинном числе.На ЕГЭ не просят округленную десятичную дробь там коннкретно пишут в обыкновенных
Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
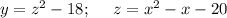
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
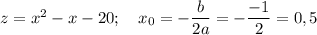- координата вершины
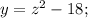z = 0 - координата вершины параболы
x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
{-3x<1.2 {x>-0.4
-0.4 2.5
-0.4<x<2.5