task/29588553 Пользуясь формулой Муавра и Бином Ньютона , выразить через степени sinφ и cosφ следующие функции кратных углов :
1) sin 4φ ; 2) cos 5φ.
* * * * * * * * * * * * * * * * * * * * * * *
* * * z₁ =a₁ + i *b₁ ; z₂ =a₂ +i*b₂ . Если z₁ = z₂ , то a₁ = a₂ и b₁ = b₂ * * *
Формула Муавра: zⁿ = ( r(cosφ +i sinφ) )ⁿ = rⁿ*[cos(nφ) + i*sin(nφ)].
1 ) (cosφ +i sinφ)⁴ = cos4φ + i * sin4φ ( а₁ ) * * * r =1 * * *
С другой стороны по формуле бинома Ньютона :
(cosφ +i sinφ)⁴=cos⁴φ+4cos³φ*(isinφ)+6cos²φ*(isinφ)²+4cosφ*(isinφ)³+(i sinφ)⁴
= cos⁴φ - 6cos²φ*sin²φ +sin⁴φ + i*( 4cos³φ*sinφ - 4cosφ*sin³φ) . ( б₁ )
Сравнивая (а₁) и (б₁) получаем :
sin4φ =4cos³φ*sinφ - 4cosφ*sin³φ || = 4sinφcosφ* (cos²φ - sin²φ) =
2sin2φ *cos2φ =sin4φ ||
2) (cosφ +i sinφ)⁵ = cos5φ + i*sin5φ ( а₂ )
(cosφ +i sinφ)⁵ =cos⁵φ +5cos⁴φ*(isinφ)+10cos³φ*(isinφ)²+10cos²φ*(isinφ)³ +
+ 5cosφ*(isinφ)⁴+ (i sinφ)⁵ = cos⁵φ - 10cos³φ*sin²φ +5cosφ*sin⁴φ +
+i*(5cos⁴φ*isinφ - 10cos²φ*sin³φ + sin⁵ φ ). ( б₂ )
Сравнивая (а₂) и (б₂) получаем :
cos5φ = cos⁵φ - 10cos³φ*sin²φ +5cosφ*sin⁴φ .
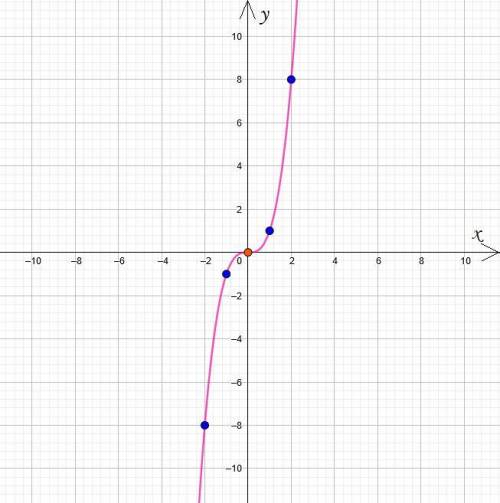
Построим график функции y = x³.
Заметим, что график функции будет пересекать ось абсцисс и ось ординат в точке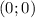 
(это несложно определить, решив два уравнения 
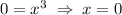и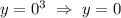 
), а также определен при всех значениях действительных значения аргумента 
.
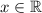Теперь можем определить несколько дополнительных точек (при желании, это можно было сделать и сразу):
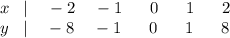
Далее проводим через все эти точки плавную линию, как показано на чертеже в приложении.
График построен!
2 )Функция четная или нечетная?
По построенному только что графику видно, что он симметричен относительно начала координат. Это означает, что рассматриваемая функция - нечетная (ведь если график симметричен относительно начала координат, то функция нечетная, а если симметричен относительно оси абсцисс, то нечетная).
Это можно было определить и аналитически. Как известно, если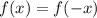 
, то функция четная, а если 
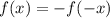, то нечетная (в противном случае функция свойством четности не обладает).
При этом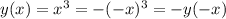 
.
Так или иначе, получаем, что функция нечетная.
3 )Принадлежат ли точки графику?
а)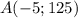 
. НЕ принадлежит.
б)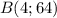 
. Принадлежит.
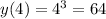
в)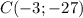 
. Принадлежит.
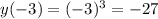
То есть графику принадлежат только точки B и C.
