- это парабола, ветви которой направлены вверх. Соответственно, если вершина этой параболы будет лежать в области определения функции y (т.е. будет выше оси абсцисс), то именно в ней достигается наименьшее значение. Если у этой параболы есть корни, то наименьшее значение функции будет равно нулю (т.к. выражение под корнем не может быть меньше нуля). Дабы убедиться, что корней нет, проверим дискриминант: 
.
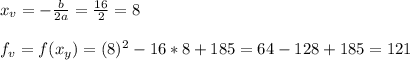
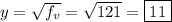
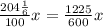
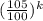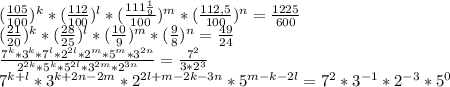
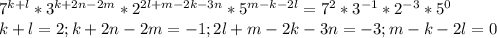
х км/ч собственная скорость лодки
(х+2) км/ч скорость лодки по течению
(х-2) км/ч скорость лодки против течения
По условию известно, что лодка против течения реки 16 км и вернулась обрано, затратив на обратный путь на 40 минут = 40/60 ч = 2/3 ч меньше, чем на путь против течения. Составим уравнение
16/(х-2) - 16(х+2) = 2/3
3*(16(х+2) - 16(х-2)) = 2(х-2)(х+2)
3*(16х + 32 - 16х + 32)= 2(х² - 4)
3* 64 = 2(х² - 4)
х² - 4 = 96
х² = 100
х = 10
ответ. 10 км/ч собственная скорость лодки.