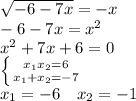
cos5x + cosx + 2cos2x = 0
2cos(5x+x/2)cos(5x-x/2) + 2cos2x = 0
2cos(6x/2)cos(4x/2) + 2cos2x = 0
2cos3x × cos2x + 2cos2x = 0
2cos2x × (cos3x + 1) = 0 | : 2
cos2x × (cos3x + 1) = 0
cos2x = 0 или cos3x + 1 = 0
2x = π/2 + πn cos3x = -1
x₁ = π/2 × 1/2 + πn × 1/2 3x = π + 2πn
x₁ = π/4 + πn/2, n∈Z x₂ = π × 1/3 + 2πn × 1/3
x₂ = π/3 + 2πn/3, n∈Z
ответ: x₁ = π/4 + πn/2, n∈Z
x₂ = π/3 + 2πn/3, n∈Z