Пусть событие А₁ - "выбран первый кубик (обычный)"
Пусть событие А₂ - "выбран второй кубик (нестандартный)"
Пусть событие В - "выпало сочетание {3; 5} при двукратном бросании кубика"
Поскольку нас интересует вероятность, связанная со вторым кубиком, то распишем вероятность события А₂В двумя :
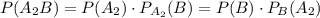
Из этого равенства выразим вероятность того, что брошен был второй кубик, при условии выпадения нужного сочетания:

Знаменатель можно расписать по формуле полной вероятности:
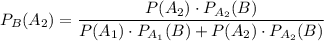
Собственно говоря, записана формула Байеса.
Выбор каждого из кубиков равновероятен:

Вероятность выпадения каждого из имеющихся чисел на первом кубике (от 1 до 6):
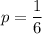
Найдем вероятность выпадения на первом кубике сочетания {3; 5}, учитывая, что этой ситуации соответствует два элементарных исхода (3; 5) и (5; 3):
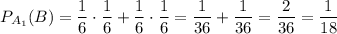
Вероятность выпадения каждого из имеющихся чисел на втором кубике (1, 3, 5):

Найдем вероятность выпадения на втором кубике сочетания {3; 5}:
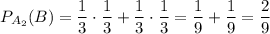
Подставим все значения:
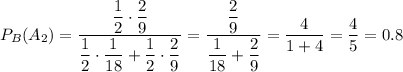
ответ: 0.8
Объяснение:
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a2 + b2 = c2.
Пошаговое доказательство:
Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:
∠ACB =∠CHA = 90º,
∠A — общий.
Также прямоугольная фигура ∆CBH подобна ∆ABC:
∠ACB =∠CHB = 90º,
∠B — общий.
Введем новые обозначения: BC = a, AC = b, AB = c.
Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.
Значит a2 = c * HB, b2 = c * AH.
Сложим полученные равенства:
a2 + b2 = c * HB + c * AH
a2 + b2 = c * (HB + AH)
a2 + b2 = c * AB
a2 + b2 = c * c
a2 + b2 = c2
Теорема доказана.