Упрощение
(4x 2 + -9) + -2 (2x + -3) + x (2x + -3) = 0
Измените порядок условий:
(-9 + 4x 2 ) + -2 (2x + -3) + x (2x + -3) = 0
Избавиться от скобок, заключающих (-9 + 4x 2 )
-9 + 4x 2 + -2 (2x + -3) + x (2x + -3) = 0
Измените порядок условий:
-9 + 4x 2 + -2 (-3 + 2x) + x (2x + -3) = 0
-9 + 4x 2 + (-3 * -2 + 2x * -2) + x (2x + -3) = 0
-9 + 4x 2 + (6 + -4x) + x (2x + -3) = 0
Измените порядок условий:
-9 + 4x 2 + 6 + -4x + x (-3 + 2x) = 0
-9 + 4x 2 + 6 + -4x + (-3 * x + 2x * x) = 0
-9 + 4x 2 + 6 + -4x + (-3x + 2x 2 ) = 0
Измените порядок условий:
-9 + 6 + -4x + -3x + 4x 2 + 2x 2 = 0
Объедините похожие термины: -9 + 6 = -3
-3 + -4x + -3x + 4x 2 + 2x 2 = 0
Объедините похожие термины: -4x + -3x = -7x
-3 + -7x + 4x 2 + 2x 2 = 0
Зерноуборочный подобные термины: 4x 2 + 2x 2 = 6x 2
-3 + -7x + 6x 2 = 0
Решение
-3 + -7x + 6x 2 = 0
Решение для переменной 'x'.
Разложите на множители трехчлен.
(-1 + -3x) (3 + -2x) = 0
Подзадача 1
Установите коэффициент '(-1 + -3x)' равным нулю и попытайтесь решить:
Упрощение
-1 + -3x = 0
Решение
-1 + -3x = 0
Переместите все термины, содержащие x, влево, все остальные термины - вправо.
Добавьте «1» к каждой стороне уравнения.
-1 + 1 + -3x = 0 + 1
Объедините похожие термины: -1 + 1 = 0
0 + -3x = 0 + 1
-3x = 0 + 1
Объедините похожие термины: 0 + 1 = 1
-3x = 1
Разделите каждую сторону на «-3».
х = -0,3333333333
Упрощение
х = -0,3333333333
Подзадача 2
Установите множитель '(3 + -2x)' равным нулю и попытайтесь решить:
Упрощение
3 + -2x = 0
Решение
3 + -2x = 0
Переместите все термины, содержащие x, влево, все остальные термины - вправо.
Добавьте «-3» к каждой стороне уравнения.
3 + -3 + -2x = 0 + -3
Объедините похожие термины: 3 + -3 = 0
0 + -2x = 0 + -3
-2x = 0 + -3
Объедините похожие термины: 0 + -3 = -3
-2x = -3
Разделите каждую сторону на «-2».
х = 1,5
Упрощение
х = 1,5
Решение
х = {-0,3333333333, 1,5}
a=1/2
Объяснение:
f(x)=2/(x+1); g(x)=a|x-3|
0≠f(x)=g(x)⇒а≠0
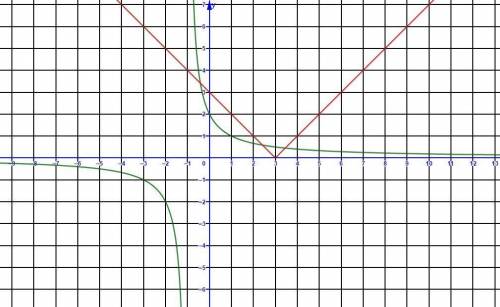
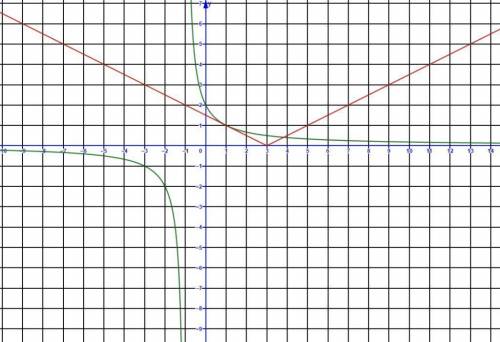
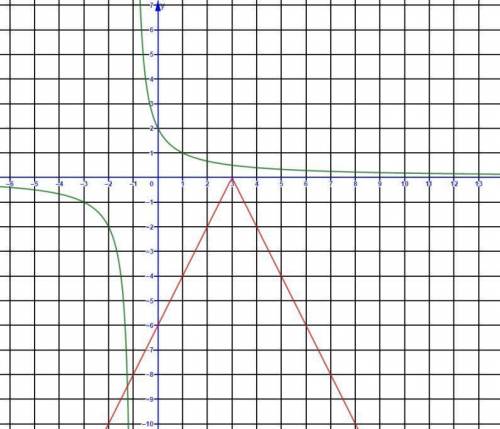
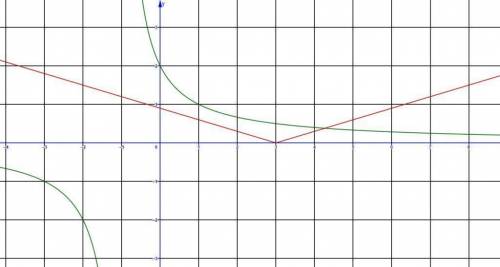
Рассмотрим расположение графиков данных функций.
Как видно из чертежей уравнение f(x)=g(x) имеет 1 решение при а<0, и не менее одного при a>0. Значить, рассматриваем только случай a>0.
Уравнение имеет ровно два решение только тогда когда левая ветка графика функции у=g(x) является касательной к графику функции у=f(x).
Эта касательная имеет вид y=-ax+3a и проходит через точку (3;0). Пусть она касается график функции f(x) в точке x₀=t.
f '(x)=(2/(x+1))'=-2/(x+1)²
f(x₀)=2/(x₀+1)=2/(t+1); f '(x₀)=-2/(x₀+1)²=-2/(t+1)²
y=f(x₀)+f '(x₀)(x-x₀)=2/(t+1)-(2/(t+1)²)(x-t)=2/(t+1)+2t/(t+1)²-(2/(t+1)²)x⇒
⇒a=2/(t+1)²; 3a=2/(t+1)+2t/(t+1)²
6/(t+1)²=2/(t+1)+2t/(t+1)²
6=2(t+1)+2t
4t=4
t=1
a=2/(t+1)²=2/(1+1)²=1/2
Дано:
S > 21см²
a = x
b = x + 4
b - ?
1) S = a · b
x · (x + 4) = 21
x² + 4x - 21 = 0
D = b² - 4ac = 16 - 4 · 1 · (-21) = 16 + 84 = 100
x₁ = (-b + √D) / 2a = (-4 + 10) / 2 = 6 / 2 = 3 (a)
x₂ = (-b - √D) / 2a = (-4 - 10) / 2 = -14 / 2 = -7 (не удовлетворяет условию)
2) b = x + 4 = 3 + 4 = 7 ⇒ чтобы S > 21см², b > 7