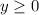Объяснение:7x2 + 10x + 5 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 102 - 4·7·5 = 100 - 140 = -40
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 23x + 15 = 0
D = b2 - 4ac = (-23)2 - 4·4·15 = 529 - 240 = 289
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 23 - √289/ 2·4 = 23 - 17 /8 = 6/ 8 = 0.75
x2 = 23 + √289 /2·4 = 23 + 17/ 8 = 40 /8 = 5
25x2 - 40x + 16 = 0
D = b2 - 4ac = (-40)2 - 4·25·16 = 1600 - 1600 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительный корень:
x = 40/ 2·25 = 0.8
найдем координаты векторов АВ и АС, выходящих из вершины А, от координат конца вычтем координаты начала.
→АВ(4-3; 6-5); →АВ(1; 1); →АС(5-3; 5-5); →АВ(2; 0);
найдем длины этих векторов. длина →АВ равна √(1²+1²)=√2; длина →АС равна √(2²+0²)=2;
Найдем скалярное произведение этих же векторов. это сумма произведений соответствующих координат.
→АВ*→АВ=1*2+1*0=2
Разделим скалярное произведение векторов на произведение их модулей, найдя косинус угла между векторами.
2/(2√2)=√2/2, значит. внутренний угол при вершине А равен 45°
ответ 45°
(квадрат числа у неотрицателен,
квадрат числа умноженный на положительное число 5 также неотрицателен, а после суммы с единицей даёт положительный результат).
Следовательно