а)х²+3>0 ⇒ х любое число,т,к х² всегда положительное
б)-х²-2≤0 ⇒-х²≤2 тоже любое,так как -х² всегад отрицательное
в)х²-4х+7≤0 нет решений,так как дискриминант <0,и при любых х левая часть положительная
г)-х²-4х≥0 ⇒ -х(х+4)≥0 ⇒ система х≤0 и х+4≥0 ⇒-4≤х≤0
система х≥0 и х+4 ≤0 ⇒ нет решений
значит -4≤х≤0
д)3х²-10х+4<1 ⇒ 3х²-10х+3<0 дискриминант равен Д=100-4*3*3=64
х₁=(10+8)/6=3 -∞ 2/6 3 +∞
х₂=(10-8)/6=2/6 || ответ 2/6< х<3
- + -
6 км/ч
Объяснение:
Пусть х км/ч - скорость второго велосипедиста,
(х + 4) км/ч - скорость первого.
Оба велосипедиста проехали по 30 км.
Запишем данные в таблицу, по строке выразим время движения каждого велосипедиста (расстояние разделить на скорость).
Время движения первого велосипедиста:
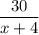 ч
ч
Время движения второго велосипедиста:
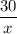 ч
ч
Известно, что первый велосипедист прибывает к финишу на 2 ч раньше второго, т.е. время движения у него меньше. Вычитаем из большего времени меньшее и получаем уравнение:
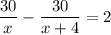
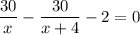
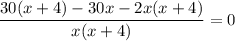
x > 0 по смыслу задачи, поэтому умножаем на знаменатель обе части уравнения.
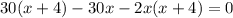
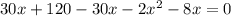
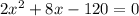
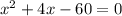
По теореме, обратной теореме Виета,
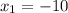 - не подходит по смыслу задачи,
- не подходит по смыслу задачи,
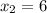 (км/ч) - скорость второго велосипедиста.
(км/ч) - скорость второго велосипедиста.

Задача. Двое рабочих изготавливают детали. Первый работал 5 ч., второй 8 ч. — и вместе выполнили 140 деталей. При этом первый за 2 ч. изготовит на 6 деталей меньше, чем второй за 3 ч. Сколько деталей за час выполняет каждый из них?
Решение. Пусть первый рабочий за час изготовлял 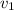 деталей, а второй рабочий
деталей, а второй рабочий 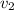 деталей. Суммарный их объём работы (по формуле
деталей. Суммарный их объём работы (по формуле 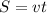 , как в задачах на движение) составит
, как в задачах на движение) составит 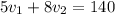 .
.
Второе условие запишется так: 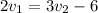
Сложим эти два уравнения в систему:
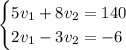
Умножим первое уравнение на 2, а второе на –5, и сложим их:
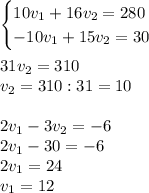
ответ: первый рабочий за час изготавливает 12 деталей, а второй — 10 деталей.
x>-3
x=>-2
x=>3
x=>2
x=>3