С увеличением числителя и знаменателя на одно и тоже число дробь увеличивается, если она правильная, и уменьшается, если она неправильная
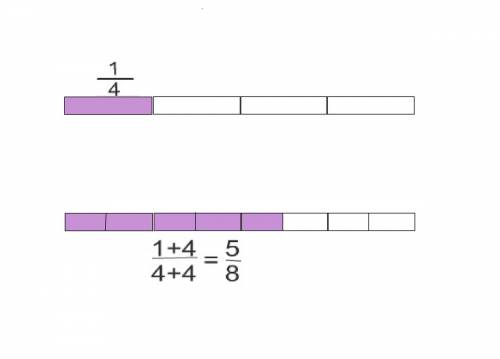
Как это выглядит на примере, смотрите на приложенном рисунке.
То-есть, увеличится количество долей (числитель), но сами эти доли ( каждая) уменьшатся в правильной дроби.
Дробь не меняется, если её и числитель, и знаменатель умножить или разделить на одно и то же число. То-есть увеличить или уменьшить в одинаковое количество раз.
О дробях и не только можно почитать в учебнике и на образовательны сайтах.
При сравнении дробей надо руководствоваться следующими правилами.
Если у дробей одинаковые знаменатели, большей дробью будет та, у которой числитель больше.
Если у дробей одинаковые числители, то большей дробью будет та, у которой знаменатель меньше.
для упрощения выражений необходимо уметь применять формулы сокращенного умножения
A)
2 1 x+1
- -
x^2 - 3x x^2 + 3x x^2 - 9 здесь в знаменателе формула разность квадратов.
(x^2 - 3x)*(x^2 + 3x)=x^4 - 9х^2 Т.о. необходимо привести к общему знаменателю, умножив и разведив дробь на недостающу часть.
2
здесь дополнительнфй множитель (x^2 + 3x)
x^2 - 3x
1
здесь дополнительный множитель (x^2 - 3x)
x^2 + 3x
Получается
2(x^2 + 3x)-1(x^2 - 3x) - x+1 = 2x^2+6x-x^2+3x - x+1 = x^2+9x-x^2(x+1)=
x^4 - 9х^2 x^2 - 9 x^2(x^2-9) x^2-9 x^2(x^2-9)
x^2+9x-x^3-x^2 = -x(x^2-9) = -x = -1/x
x^2(x^2-9) x^2(x^2-9) x^2
Б)
2y + 1 + y+2 - 1 = (в знаменателе выводим у за скобки,
y^2+3y 3y - y^2 y (у+3)(3-у)=9-у^2 )
= (2y+1)(3-y) +(y+2)(3+y)-(9-y^2) = 6y+3-2y^2-y+3y+6+y^2+2y-9+y^2 =
y(y+3)(3+y) y(9-y^2)
10y = 10
y(9-y^2) 9-y^2
в следующих двух выражения применяется формула сокращенного умножения разность и сумма кубов.
В)
a^2 + 16a +12 - 2 - 3a - 3 =
a^3 - 8 a^2 + 2a + 4 a - 2
a^3 - 8=(a - 2)( a^2 + 2a + 4) опираясь на эту формулу, приводим дроби к общему знаменателю
(a^2 + 16a +12)-(2 - 3a)(a - 2)-3( a^2 + 2a + 4)= a^+16a+12-2a+3a^2+4-6a-3a^-6a-12
( a^2 + 2a + 4)(a - 2) ( a^2 + 2a + 4)(a - 2)
=a^2-2a = a(a-2) = a
( a^2 + 2a + 4)(a - 2) ( a^2 + 2a + 4)(a - 2) a^2 + 2a + 4
Г)
2 + 4b^2 + 18 - 1
4b^2 - 6b + 9 8b^3 + 27 2b + 3
8b^3 + 27=(4b^2 - 6b + 9)(2b + 3)
= 2(2b + 3)+4b^2 + 18 - (4b^2 - 6b + 9) =4b+6+4b^2+18-4b^2+6b-9 = 10b+15 =
(4b^2 - 6b + 9)(2b + 3) (4b^2-6b+9)(2b + 3) (4b^2-6b+9)(2b+3)
= 5
4b^2-6b+9
сравнивать можно с числовой окружности. Нанесём на числовую окружность число 7.5.(рисунок сейчас вышлю). Учитывая, что синус - ордината точки, а косинус - абсцисса точки, сравним абсциссу и ординату одной и той же точки. Получаем, что sin 7.5 > cos 7.5(по рисунку это прекрасно видно)