Задача 1.
В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует это сделать?
Решение. Старостой может быть выбран любой из 30 студентов, заместителем - любой из оставшихся 29, а профоргом – любой из оставшихся 28 студентов, т.е. n1=30, n2=29, n3=28. По правилу умножения общее число выбора старосты, его заместителя и профорга равно N=n1n2n3=302928=24360.
Задача 2.
Два почтальона должны разнести 10 писем по 10 адресам. Сколькими они могут распределить работу?
Решение. Первое письмо имеет n1=2 альтернативы – либо его относит к адресату первый почтальон, либо второй. Для второго письма также есть n2=2 альтернативы и т.д., т.е. n1=n2=…=n10=2. Следовательно, в силу правила умножения общее число распределений писем между двумя почтальонами равно .
Задача 3.
В ящике 100 деталей, из них 30 – деталей 1-го сорта, 50 – 2-го, остальные – 3-го. Сколько существует извлечения из ящика одной детали 1-го или 2-го сорта?
Решение. Деталь 1-го сорта может быть извлечена го сорта По правилу суммы существует извлечения одной детали 1-го или 2-го сорта.
Задача 4.
Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число равно
Задача 5.
В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по всем номинациям установлены различные премии?
Решение. Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций, как составом, так и их порядком. Так как каждый фильм может получить призы как по одной, так и по нескольким номинациям, то одни и те же фильмы могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 10 элементов по 5:
Задача 6.
В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетания из 16 элементов по 2. Их число равно
Вот надеюсь если не правильно напиши в комментариях (толь нужно будет написать где неправильно и почему)
Объяснение:
f'x = (ctg(x^2 × y))' = -1/(sin^2 (x^2 × y)) × (x^2×y)' = -1/(sin^2 (x^2 × y)) × 2 × x × y = - (2×x×y) / (sin^2 (x^2 × y))
f'y = ctg(x^2 × y))' = -1/(sin^2 (x^2 × y)) × (x^2×y)' = -1/(sin^2 (x^2 × y)) × x^2 = -(x^2) / (sin^2 (x^2 × y))
f"xx = ( -(2×x×y) / (sin^2 (x^2 × y)) )' = - (2×x×y)' × 1/ (sin^2 (x^2 × y)) - (2×x×y) × (1/(sin^2 (x^2 × y)))' = - (2×y) / (sin^2 (x^2 × y)) - (2×x×y) × ( -2/(sin^3 (x^2 ×y)) ) × cos(x^2 × y) × 2 × x × y = - (2×y) / (sin^2 (x^2 × y)) + (8×x^2×y^2) × (1/(sin^3 (x^2 ×y)) ) × cos(x^2 × y) = - (2×y) / (sin^2 (x^2 × y)) + ( 8×x^2×y^2 × cos(x^2 × y) ) / (sin^3 (x^2 ×y))
f"yy = (-(x^2) / (sin^2 (x^2 × y)))' = -(x^2) × (-2) × (sin^(-3) (x^2 × y)) × cos (x^2 × y) × x^2 = ( 2 × x^4 × cos (x^2 × y) ) / (sin^3 (x^2 × y))
f"xy = f"yx = - (2×x) / (sin^2 (x^2 × y)) - (2×x×y) / (sin^3 (x^2 × y)) × (-2 × cos(x^2×y) × x^2) = - (2×x) / (sin^2 (x^2 × y)) + 4 (x^3 × y × cos(x^2×y)) / (sin^3 (x^2 × y))
1)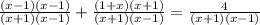
Область определения: x ≠ -1; x ≠ 1
(x - 1)^2 + (x + 1)^2 = 4
x^2 - 2x + 1 + x^2 + 2x + 1 - 4 = 0
2x^2 - 2 = 0
2(x^2 - 1) = 0
2(x + 1)(x - 1) = 0
x1 = -1; x2 = 1
Оба корня не подходят по области определения.
Решений нет.
2)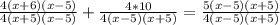
Область определения: x ≠ -5; x ≠ 5
4(x^2 + x - 30) + 40 = 5(x^2 - 25)
4x^2 + 4x - 120 + 40 = 5x^2 - 125
0 = x^2 - 4x - 45
(x - 9)(x + 5) = 0
x = -5 не подходит по области определения
x = 9 подходит.
3)
Область определения x ≠ 4; x ≠ 9
x^2 - 3x - 54 - 50 + x^2 + x - 20 = 0
2x^2 - 2x - 124 = 0
x^2 - x - 62 = 0
D = 1 - 4(-62) = 249
x1 = (1 - √249)/2; x2 = (1 + √249)/2
Но я предполагаю, что в задаче опечатка, должно быть:
Тогда получается уравнение
x^2 - x - 12 = 0
(x - 4)(x + 3) = 0
Подходит только корень
x = -3