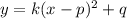, где q определяет ординату (т.е. значение по оси у) точки экстремума, -р определяет абсциссу (т.е. значение по оси х) точки экстремума, а k - это коэффициент, который показывает, насколько сжаты (k>1) или расширены (k<1) ветви заданной параболы относительно параболы с уравнением y=x². Положительный знак k говорит о том, что ветви параболы будут направлены вверх и экстремум является минимумом, а отрицательный знак k показывает, что ветви параболы направлены вниз и экстремум является максимумом. Фактически, k определяет точки, отличные от точки экстремума, через которую обязаны пройти ветви параболы.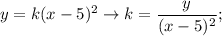
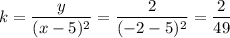
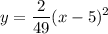
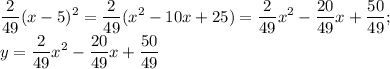
![\displaystyle ax^2+bx+c= a(x^2+ \frac{b}{a}x+ \frac{c}{a})= \\ a\left[\left( x^2+ 2\frac{b}{2a}x+\left( \frac{b}{2a}\right)^2\right)+\left(-\left( \frac{b}{2a}\right)^2+ \frac{c}{a}\right)\right]= \\ a\left[\left( x+\frac{b}{2a}\right)^2+\left(-\left( \frac{b}{2a}\right)^2+ \frac{c}{a}\right)\right]=a\left( x+\frac{b}{2a}\right)^2+\left(c- \frac{b}{4a}\right); \\ k=a; \quad p=\frac{b}{2a}; \quad q=c- \frac{b}{4a}](/tpl/images/0410/1947/8db1c.png)
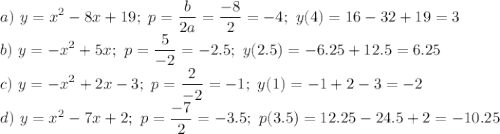
(3a-b)(5b-a)=15ab-3a^2-5b^2+ab=16ab-3a^2-5b^2
4a(a-b)-(a+b)(4a-b)=4a^2-4ab-4a^2+ab-4ab+b^2=b^2-7ab
(3a-2)(a+3)+(a-4)(1-3a)=3a^2+9a-2a-6+a-3a^2-4+12a=20a-10
(2a-3)^2=4a^2-12a+9
3(x-1)(x+2)=(3x-3)(x+2)=3x^2+6x-3x-6=3x^2-3x-6
(3x-7)(2-x)=6x-3x^2-14+7x=-3x^2-7x-14
3x(x-y)-(x-y)(3x-y)=3x^2-3xy-3x^2+xy+3xy-y^2=xy-y^2
(5x-1)(x+2)+(x-1)(2-5x)=5x^2+10x-x-2+2x-5x^2-2+10x=21x-4
(3x-2)^2=9x^2-12x+4
2(x-3)(x+1)=(2x-6)(x+1)=2x^2+2x-6x-6=2x^2-4x-6