Построить треугольник вершины которого находятся в точках a(m+1; n+1),b(m; -n),c(-m; n)и найти 1 уравнения стороны ab 2 уравнения медианы,проведенной из вершины с, 3 координату точки пересечения медиан: 4 уравнения высоты,опущенной из вершин b на сторону ac и ее длину: 5 уравнения прямой,проходящий через точку с параллельно прямой ab, 6 площадь треугольника :
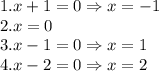
![(-\infty,-1] \\1.x+1\Rightarrow - \\2. x\Rightarrow - \\3.x-1 \Rightarrow - \\4.x-2 \Rightarrow-](/tpl/images/0606/9640/7515c.png)
![[-1,0] \\1. x+1 \Rightarrow + \\2. x \Rightarrow- \\3.x-1 \Rightarrow - \\4.x-2 \Rightarrow -](/tpl/images/0606/9640/01704.png)
![[0,1] \\1. x+1 \Rightarrow + \\2.x \Rightarrow + \\3. x-1 \Rightarrow - \\4. x-2 \Rightarrow -](/tpl/images/0606/9640/a22f7.png)
![[1,2] \\1. x+1 \Rightarrow + \\2.x \Rightarrow + \\3.x-1 \Rightarrow+ \\4.x-2 \Rightarrow -](/tpl/images/0606/9640/70ba8.png)
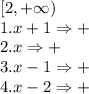
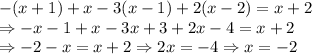
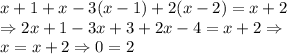
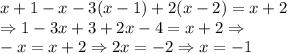
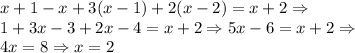
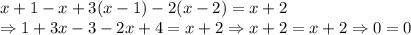
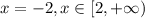
(19, 342), (20, 180), (21, 126), (22, 99), (24, 72), (27, 54) и (36, 36)
Объяснение:
Представим уравнение в другом виде:
324 можно разложить на простые множители: 2²·3⁴
Значит m-18 должно содержать эти множители. Он может быть равен 1,2,3,4,6,9,18,108 и 324. Соответствующие m для этого: m = 19,20,21,22,24,27,36,126 и 342
При последовательной подстановке этих чисел в уравнении нахождения чисел n, мы получаем: n = 342, 180, 126, 99, 72, 54, 36, 21 и 19. Среди них подходят пары (19, 342), (20, 180), (21, 126), (22, 99), (24, 72), (27, 54) и (36, 36)