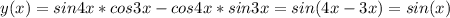
есть 
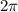
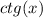равен 
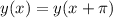
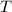- искомый период, тогда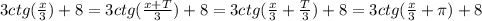
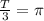
относительно оси OX на 8 единиц вверх, также не влияя на период
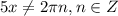
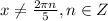
- это симметричное относительно начала координат множество точек,
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
сумма цифр равна 10, т.е х+у=10
переставили цифры: ух, теперь ух=10у+х
цифру единиц увеличили на 1, т.е. 10у+х+1
и раз новое число в 2 раза больше изначального можно составить уравнение:
10у+х+1=2(10х+у)
10у-2у=20х-х-1
8у=19х-1
выразим из первого уравнения х+у=10: у=10-х
8(10-х)=19х-1
19х+8х=80+1
27х=81
х=3
тогда у=10-х=10-3=7
получилось число 37
проверяем сумма цифр: 3+7=10
Если цифры этого числа переставить и цифру единиц нового числа увеличить на 1: получаем 73+1=74
и 74/2=37