Две машинистки, работая вместе, печатают в час 44 страницы текста. первые 25% двухсотстраничной рукописи печатала первая машинистка, затем к ней присоединилась вторая, а последние 20% текста печатала только вторая машинистка. сколько страниц в час печатает каждая машинистка, если на на перепечатывание всей рукописи ушло 6ч 40 мин и первая машинистка работает быстрее второй?

👇

Ответ:

дашуля296

13.11.2020

25% 200-страничной рукописи - значит 50 страниц.
20% текста - это 40 страниц
значит 110 страниц они печатали одновременно

Х стр/час печатает 1 машинистка
У стр/час печатает 2 машинистка

Х+У = 44

50/Х + 110/(Х+У) + 40/У = 6+2/3 (записать как 6целых 2/3)

Систему-то решите надеюсь? :-)

PS в итоге получилось 2 скорости у У-машинистки: 24 стр/час и 17,6 стр/час.
Значит у Х-машинистки (которая 1-я была) скорости 20 стр-час и 26,4 стр/час соответственно

По условию нам известно, что Х-машинистка печатает БЫСТРЕЕ, значит первый вариант не подходит, правильный ответ: 26,4 страницы в час печатает 1 машинистка и 17,6 вторая.

4,5(98 оценок)

Открыть все ответы

Ответ:

lipaalexandrova

13.11.2020

Есть формула 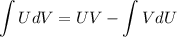$\displaystyle \int UdV= UV - \int VdU$

Но напрямую я её использовать не очень люблю.

Проще использовать такой подход (он, конечно, на формуле основан)

1. "Разрезать" функцию на 2 части: одну, которую будем дифференцировать, а другую - интегрировать. Понятно, что это разбиение часто основывается на том, какую функцию проще интегрировать, так как продифференцировать можно любую (но иногда, как во 2-м примере, будем смотреть, какую функцию лучше дифференцировать).

2. В столбик написать обе получившиеся функции (ту, которую интегрируем, с дифференциалом запишем, естественно). Отчертить большой чертой и справа напротив каждой функции написать результат того, что мы с ней делаем (в одном случае результат интегрирования, а в другом дифференцирования).

3. А дальше итоговый интеграл будет равен "функция на функцию" (это будет крест накрест, где нет дифференциалов) минус интеграл от произведения функций справа.

Попробую на примере показать:

а) есть интеграл 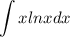$\displaystyle \int x lnx dx$

Здесь удобнее интегрировать логарифм, а дифференцировать

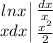
$\displaystyle \left.\begin{matrix}lnx\\ xdx \end{matrix}\right| \begin{matrix}\frac{dx}{x}\\ \frac{x^2}{2} \end{matrix}$

Ну вот как-то так. И теперь сам интеграл:

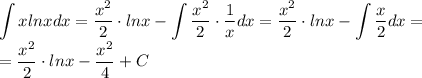
$\displaystyle \int xlnxdx = \frac{x^2}{2}\cdot lnx-\int \frac{x^2}{2}\cdot \frac{1}{x}dx=\frac{x^2}{2}\cdot lnx-\int \frac{x}{2}dx=\\=\frac{x^2}{2}\cdot lnx-\frac{x^2}{4}+C$

Надеюсь, что стало понятнее.

б) здесь придется интеграл по частям брать аж 2 раза, но ничего страшного, возьмем.

Сам интеграл 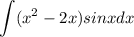$\displaystyle \int(x^2-2x)sinxdx$

Здесь понятно, что тригонометрия будет давать тригонометрию что при интегрировании, что при дифференцировании, а вот многочлен уже при втором дифференцировании даст константу, так что его и будем дифференцировать.

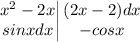
$\displaystyle \left.\begin{matrix}x^2-2x\\ sinxdx \end{matrix}\right| \begin{matrix}(2x-2)dx\\ -cosx \end{matrix}$

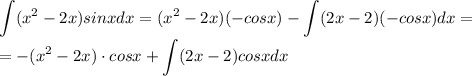
$\displaystyle \int (x^2-2x)sinxdx = (x^2-2x)(-cosx) - \int (2x-2)(-cosx)dx = \\= -(x^2-2x)\cdot cosx + \int (2x-2)cosxdx$

Надо лишь решить ещё один интеграл, причем абсолютно так же.

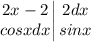
$\displaystyle \left.\begin{matrix}2x-2\\ cosxdx \end{matrix}\right| \begin{matrix}2dx\\ sinx \end{matrix}$

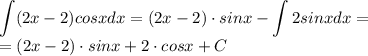
$\displaystyle \int(2x-2)cosxdx = (2x-2)\cdot sinx - \int 2sinxdx = \\ = (2x-2)\cdot sinx+2\cdot cosx + C$

Ну и соберем все теперь:

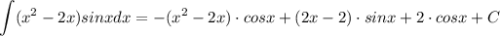
$\displaystyle \int(x^2-2x)sinxdx = -(x^2-2x)\cdot cosx + (2x-2)\cdot sinx + 2\cdot cosx + C$

4,5(90 оценок)

Ответ:

VasyaPumpkin

13.11.2020

В обоих случаях нужно делать замену переменной.

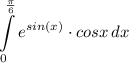
$\displaystyle \int\limits^{\frac{\pi}{6}}_0 {e^{sin(x)}}\cdot cosx \, dx$

Что тут можно предпринять? Известно, 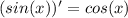(sin(x))' = cos(x) , вот и сделаем замену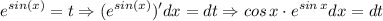 $\displaystyle e^{sin(x)} = t \Rightarrow (e^{sin(x)})'dx=dt \Rightarrow cos\, x\cdot e^{sin \, x} dx=dt$

Вообще идеально, получим простейший интеграл. Так как это определенный интеграл, то обратную замену можно не делать, а просто пересчитать пределы по самой замененной функции

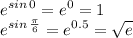
$\displaystyle e^{sin\, 0} = e^0=1 \\ e^{sin \, \frac{\pi}{6}} = e^{0.5}=\sqrt{e}$

То есть пределы станут: 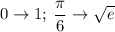$\displaystyle 0 \to 1; \: \frac{\pi}{6} \to \sqrt{e}$

А теперь сам интеграл 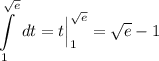$\displaystyle \int\limits^{\sqrt{e}}_1 {} \, dt = t \Big|\limits^{\sqrt{e}}_1 = \sqrt{e} -1$

Теперь следующий интеграл:

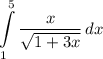
$\displaystyle \int\limits^5_1 {\frac{x}{\sqrt{1+3x}} } \, dx$

Что можно такого заменить? Попробуем взять корень, его производная даст тот же корень в знаменателе, да и сам вполне нормально выражается, делаем:

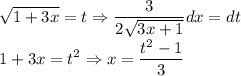
$\displaystyle \sqrt{1+3x}=t \Rightarrow \frac{3}{2\sqrt{3x+1}}dx=dt \\ 1+3x=t^2 \Rightarrow x=\frac{t^2-1}{3}$

Заодно сразу новые пределы посчитаем:

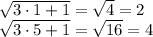
$\sqrt{3\cdot 1+1} = \sqrt{4}=2 \\ \sqrt{3\cdot 5+1} = \sqrt{16}=4$

То есть 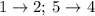$1 \to 2; \: 5 \to 4$

Теперь подставляем и смотрим, что получается:

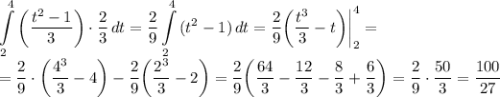
$\displaystyle \int\limits^4_2 {\bigg(\frac{t^2-1}{3} \bigg)\cdot \frac{2}{3} } \, dt=\frac{2}{9}\int\limits^4_2 {(t^2-1)} \, dt =\frac{2}{9}\bigg(\frac{t^3}{3}-t \bigg) \bigg|\limits_2^{4}=\\=\frac{2}{9}\cdot \bigg(\frac{4^3}{3}-4\bigg)-\frac{2}{9}\bigg(\frac{2^3}{3}-2 \bigg)=\frac{2}{9}\bigg(\frac{64}{3}-\frac{12}{3}-\frac{8}{3}+\frac{6}{3} \bigg)=\frac{2}{9}\cdot \frac{50}{3}=\frac{100}{27}$

Можно, конечно, было и получить неопределенный интеграл и в него подставить старые пределы, но пересчет на новые позволяет не совершать часть действий

4,5(46 оценок)

Это интересно:

Кулинария-и-гостеприимство

25.08.2021

Как сделать чай из роз: полезные рецепты и особенности приготовления...

Искусство-и-развлечения

07.05.2022

Как играть на тромбоне: советы и рекомендации для начинающих...

12.09.2020

Как остановить человека, который задирает вас...

Компьютеры-и-электроника

26.04.2020