Первоначальная функция имеет следующею область определения:
Построим схематично преобразованную функцию Y и наложим ограничение. График функции Y это гипербола, которая лежит в 1 и 3 четвертях относительно следующих прямых: y=0; x=2/3, которые так же являются асимптотами. Пересечение с осями координат:
См. вниз. (1)
Что бы понять как именно убывает функция найдём не сколько точек.
У получившейся кривой есть точка, которая равноудалена от двух асимптот точка A. См. вниз (2)
Найдём координаты этой точки и ещё пару точек кривой, чтобы понять как быстро функция убывает.
1) 150*(1-35:100)+250+200=547.5 рублей потратит клиент при условии скидки 35% на звонки внутри сети в месяц 2) 150+(1-25:100)*250+200=537.5 рублей потратит клиент при условии скидки 25% на звонки абонентам других компаний в месяц 3) 150+250+(1-30:100)*200=540 рублей потратит клиент при условии скидки 30% на отправку текстовых сообщений 4) 547.5>540>537.5 - значит лучшая скидка для клиента єто 25% на звонки абонентам других компаний 5) 25:100*250=62.5 р=62р 50 коп. - составит скидка ответ: 62р 50 коп.
Тождества Два выражения, соответственные значения которых равны при любых значениях переменных, называютсятождественно равными.
Например выражения 4(a + b) и 4a + 4b являются тождественно равными, а выражения 3a + b и 3ab - нет.
Равенство, верное при любых значениях переменных, называется тождеством.
Тождеством считают и верные числовые равенства.
Тождествами также являются равенства, выражающие основные свойства действий над числами: a + b = b + a ab = ba (a + b) + c = a + (b + c) (ab)c = a(bc) a(b + c) = ab + ac
Тождественные преобразования Замену одного выражения другим, тождественно равным ему выражением называют тождественным преобразованием или просто преобразованием выражения.
Тождественные преобразования выражений с переменными выполняются на основе основный свойств действий над числами.
Тождественные преобразования выражений широко применяются при вычислении значений выражений и решении других задач.
Некоторые тождественные преобразования Вам уже приходилось выполнять, например приведение подобных слагаемых и раскрытие скобок.Напомним правила выполнения этих преобразований:чтобы привести подобные слагаемые, нужно сложить их коэффициенты и результат умножить на общую буквенную частьесли перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобкиесли перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки
Первоначальная функция имеет следующею область определения: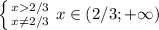
Построим схематично преобразованную функцию Y и наложим ограничение. График функции Y это гипербола, которая лежит в 1 и 3 четвертях относительно следующих прямых: y=0; x=2/3, которые так же являются асимптотами. Пересечение с осями координат: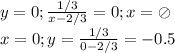
См. вниз. (1)
Что бы понять как именно убывает функция найдём не сколько точек.
У получившейся кривой есть точка, которая равноудалена от двух асимптот точка A. См. вниз (2)
Найдём координаты этой точки и ещё пару точек кривой, чтобы понять как быстро функция убывает.
Существует только x>2/3.
Для ясности нарисую табличку.
См. вниз (3)
Теперь строим график нашей функции.
См. вниз (4)