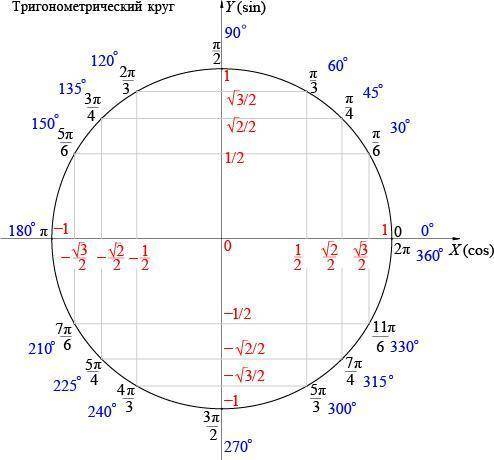
S9 = - 711.
Объяснение:
1. В арифметической прогрессии (аn)
a1 = -143, a2 = -127, тогда d = a2 - a1 = -127 - (-143) = -127+143 = 16.
2. Sn = (2•a1 +d(n-1))/2•n;
В нашем случае
Sn = (2•(-143)+16•(n-1))/2•n = (-143+8n-8)•n = (-151+8n)•n = -151n + 8n^2.
2. Рассмотрим функцию
S = 8x^2 - 151x. Она квадратичная, графиком является парабола, ветви которой направлены вверх, т.к. а= 8, 8>0. Своего наименьшего значения функция достигает в вершине параболы.
х вершины = -b/2a = 151/16 = 8 13/16.
При х ≤ 8 13/16 функция убывает, при х ≥ 8 13/16 функция возрастает.
3. Наша функция
Sn = -151n + 8n^2 определена для натуральных значений n, поэтому наименьшее значение выбираем из S8 и S9.
S8 = -151•8 + 8•64 = -1208 + 512 = -696;
S9 = -151•9 + 8•81 = -1359 + 648 = -711.
Получили, что сумма девяти первых членов прогрессии наименьшая, её значение равно -711.
(Примечание:
Можно было, не сравнивая S8 и S9, показать, что наименьшей окажется S9, т.к. 9 ближе к значению абсциссы вершины параболы 8 13/16, чем 8. Но, на мой взгляд, дальнейшие строгие рассуждения со ссылкой на симметричность параболы относительно прямой х = 8 13/16 не просты.)
1) 90°<143°<180° - Вторая четверть, sin143°>0 , cos143°<0 , tg143°<0 , ctg143°<0
2) -243° - вторая четверть. sin(-243°)>0 , cos(-243)°<0 , tg(-243°)<0 , ctg(-243°)<0
3) 735° . Весь круг - 360° , 360 * 2 =720° + ещё немного. Это значит, что 735° в 1 четверти. sin735°>0, cos735°>0 , tg735° и ctg 735° > 0.
4)-735°. -735° в 4 четверти. sin(-735°)<0 , cos(-735°)>0 + , tg(-735°) и ctg(-735°) < 0.
5) 300° - 3 четверть , sin(300°)<0 , cos(300°)<0 + , tg(300°) и ctg(300°) > 0 .
6) 
, 
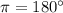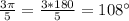∈ 2 четверти,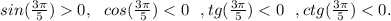 
7) 
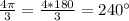, ∈ 3 четверти ,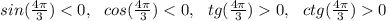 
8) 1 радиан ≈ 57° . -0,5 радиан - 4 четверть. sin(-0,5)<0 , cos(-0,5)>0 , tg(-0,5) < 0 ,ctg (-0,5) <0
9) 4 радиана ∈ 3 четверти (4*57°≈228° ), sin4<0 , cos4<0 , tg4>0 , ctg4>0
10) -7,3 ∈ 4 четверти (-7,3*57°≈-416,1°), sin(-7,3) <0 , cos(-7,3) >0 , tg(-7,3) <0 , ctg(-7,3) <0.
