Берем производную:
y' = 10x
10x = 0
x = 0
Смотрим как ведет себя производная в районе этой точки
При x < 0 y' < 0 => исходная функция убывает на интервале (-бесконечность;0)
При x > 0 y' > 0 => исходная функция возрастает на интервале (0;+бесконечность)
Это значит, что наименьшее значение на отрезке [-1;2] функция достигает при x = 0, то есть y(0)=15 - наименьшее значение
Свое наибольшее значение функция достигает на одном из концов отрезка:
y(-1) = 20
y(2)=35 - наибольшее значение функции на отрезке [-1;2\
Объяснение:
ответ: 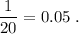
Нам благоприятствуют 45 чисел. Возьмем любую цифру и начнем в ней строить всевозможные подходящие числа. Для каждого из чисел от 3 до 7 включительно есть по 2*3=6 пар (два числа и три их расположения). Для цифр 1, 8, 9 есть по три числа (131, 311, 113 и т. д.). Для цифры 0 - одно (200), а для 2 - пять чисел (220, 202, 224, 242, 422). Итого:
5 * 6 + 3 * 3 + 1 + 5 = 45 (чисел).
А всего трехзначных чисел:
9 * 10 * 10 = 999 - 100 + 1 = 900.
Тогда искомая вероятность равна:
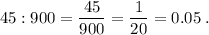
Примечание:
Вот эти 45 чисел:
113, 131, 311, 220, 202, 224, 242, 422, 331, 313, 133, 335, 353, 533, 442, 424, 244, 446, 464, 644, 553, 535, 355, 557, 575, 755, 664, 646, 466, 668, 686, 866, 775, 757, 577, 779, 797, 977, 886, 868, 688, 997, 979, 799, 200.
= 8+Ln(6/3)=8+Ln2