Нужно! ! в арифметической прогрессии сумма третьего и девятого членов равна 6, а их произведение( умножение×××) ровно 135/6. найдите сумму первых пятнадцати членов прогрессии.

👇

Ответ:

Bibika2005

16.09.2022

Пусть а1- первый член арифметической прогрессии , d- разность прогрессии. Имеем систему из двух уравнений : а3+а9=6 и а3·а9=135/6
выразим а3 и а9 через первый член и разность прогрессии :
а3=а1+2d и a9= a1+8d и подставим в первое уравнение системы , получаем : а1+2d+a1+8d=6
2a1+10d=6
a1+5d=3
a1=3-5d
Сделаем подстановку во втором уравнении :
(a1+2d)(a1+8d)=6 подставим а1=3-5d и получим
(3-5d+2d)(3-5d+8d)=6
(3-3d)(3+3d)=6
9-9d²=6
9d²=3
d²=1/3
d=√1/3=√3/3 или d=-√1|3=√3|3
1) При d=√3/3 а1=3-5·√3/3
По формуле суммы арифметической прогрессии имеем :
S15=(2(3-5√3/3)+√3/3·14)/2·15=(9-2√3)·5=45-10√3
2) При d=-√3/3 a1=3+5√3/3
S15=45-10√3

4,7(66 оценок)

Открыть все ответы

Ответ:

радмир1402

16.09.2022

$x^3+3x+2\sqrt[3]{x-4} -34=0$

Запишем уравнение в виде:

$x^3+3x -34=-2\sqrt[3]{x-4}$

Пусть левая и правая часть равны у. Тогда получим систему:

$\begin{cases} y=x^3+3x -34\\y=-2\sqrt[3]{x-4}\end{cases}$

Рассмотрим каждое уравнение как функцию.

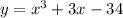y=x^3+3x -34 - возрастающая функция, так как это кубическая парабола с положительным старшим коэффициентом

$y=-2\sqrt[3]{x-4}$ - убывающая функция, так как корень нечетной степени имеет сомножителем отрицательное число

Графически возрастающая и убывающая функция могут пересекаться не более чем в одной точке.

В данном случае, понимая, что и область определения и область значений каждой функции представляют собой все действительные числа можно сказать, что такое пересечение обязательно произойдет.

Таким образом, если найден некоторый корень этого уравнения, то других корней у уравнения нет.

Подберем корень. Удобно начать проверку с "красивых значений". Например, будем выбирать х так, чтобы под знаком корня получался куб некоторого целого числа.

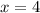Пусть $\sqrt[3]{x-4} =\sqrt[3]{0}$ , то есть x=4 . Проверим, является ли это число корнем:

$4^3+3\cdot4+2\sqrt[3]{4-4} -34=64+12+2\cdot0-34=42\neq 0$ - не корень

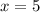Пусть $\sqrt[3]{x-4} =\sqrt[3]{1}$ , то есть x=5 . Проверим, является ли это число корнем:

$5^3+3\cdot5+2\sqrt[3]{5-4} -34=125+15+2\cdot1-34=108\neq 0$ - не корень

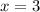Пусть $\sqrt[3]{x-4} =\sqrt[3]{-1}$ , то есть x=3 . Проверим, является ли это число корнем:

$3^3+3\cdot3+2\sqrt[3]{3-4} -34=27+9+2\cdot(-1)-34=0$ - корень

Таким образом, уравнение имеет единственный корень 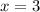x=3

ответ: 3

4,6(61 оценок)

Ответ:

karolinamurzak

16.09.2022

Предположим , что степень полинома P(x) не равна степени полинома: x*Q(x).

Тогда степень полинома:

P(x) + x*Q(x) равна либо степени полинома P(x) либо x*Q(x) , в зависимости от того степень какого полинома больше. Но тогда по условию полином большей степени должен иметь 2 степень. Соответственно полином меньшей степени имеет 1 или 0 степень. Но тогда полином : x*P(x)*Q(x) имеет 2 или 3 степень, что невозможно , тк по условию : P(x)*x*Q(x) должен иметь 9+1=10 степень. То мы пришли к противоречию .

Значит степени полиномов P(x) и x*Q(x) должны быть равны.

Тогда тк степень x*P(x)*Q(x) равна 10. То степень полинома P(x) равна:10/2=5

2) Полином :

P(x) +Q(x) имеет степень 3, а полином

P(x)-Q(x) имеет степень 5.

Тогда сумма и разность этих полиномов имеет 5 степень:

То есть 2*P(x) имеет 5 степень и 2*Q(x) имеет 5 степень.

Тогда P(x)*Q(x) имеет 10 степень.

4,5(57 оценок)

Это интересно:

31.01.2021

Как бороться со стрессом с помощью еды...