1) Заметим, что, если в кучке осталось 2 спички, никому из игроков не выгодно брать из нее спичку, т.к. следующим ходом противник заберет оставшуюся спичку и победит. Тогда, если есть кучка с 1 спичкой, забираем спичку, если же есть спички числом спичек, большим 2, берем спичку из любой.
Если во всех кучках осталось по 2 спички, то было совершено 99*101=9999 ходов, а значит последнюю спичку в данный момент забрал начинающий. Тогда на 10000 ход второй вынужден забрать спичку из кучки с 2 спичками. А дальше игра оканчивается ничьей.
А значит ответ нет.
2) Заметим, что искомая сумма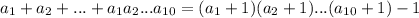 
.
И правда. Пусть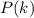 
- сумма всех комбинаций по 1 ... по k элементов. Тогда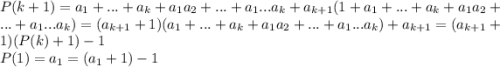 
Т.к. числа отрицательны, то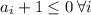 
Если хотя бы одно из 
, вся сумма равна -1.
В остальных случаях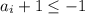 
- всегда отрицательное. Но произведение 10 целых отрицательных чисел положительно, причем не меньше 1. Противоречие с тем, что 
.
А тогда сумма могла равняться только -1
№5 4а(а-5)-(а+3)^2=4a^2 - 20a - a^2 -6a - 9 = 3a^a - 26a - 9
№6 7(х-р)^2+14хр = 7x^2 - 14xp - 7p^2 +14xp = 7(x^2 - p^2)
№11(упростите выражение)
(5с-b)^2(5c+b)^2 = (25c^2 -b^2)^2
№13(разложить на множители
x^2y+xy^2+x^3+y^3 = x^3 + x^2y + xy^2 +y^3 = (x + y)^3 - 2xy(x+y)
№14(найдите значение выражения)
p^2+4b^2,если р+2b=8,рb=10 (ты уверена что правильно записала последнее?)