Объяснение:
А) Подставляем везде места х цифру 0
3×0/0^2-3×0 = 0
1) 3×0=0
2) 0^2=0
3) 3×0=0
ответ: 0
Подставляем цифру 13 места х
3×13/13^2-3×13= 39/169-39 = 39/130 = 0.3 или 3/10
1) 3×13=39
2) 3^2=169
3) 169-39=130
4) 39:130=0.3 , а если в дробях то 39/130 сокращаем на 13=3/10
ответ: 0.3 или можно также записать 3/10
Б) Подставляем вместо х цифру 3
12(3-3)/24=12/24=2
1) Всегда сначала решаем то что в скобках (3-3) =0
2) Остаётся 12/24 здесь сократим на 12 будет =2
ответ: 2
Подставляем 5 вместо х
12(5-3)/24= 12×2/24=24/24=1
1) Сначала то что в скобках (5-3)=2
2) 12×2=24
3) 24/24=1
ответ:1
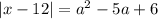
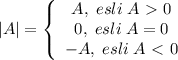
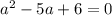 при
при 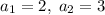 .
.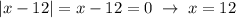 .
.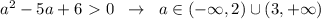
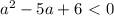 , то решений уравнение не будет иметь,так как модуль не может принимать отрицательные значения. Это будет в случае
, то решений уравнение не будет иметь,так как модуль не может принимать отрицательные значения. Это будет в случае 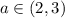 .
.
решение представлено на фото