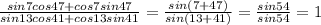
1. Область определения - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет
2. Пересечение с осью Х. Y=0
При х1 = x2 = - 2, x3 = 1
3. Пересечение с осью У. У(0) = -4
4. Поведение на бесконечности.
limY(-∞) = - ∞ и limY(+∞) = +∞
Горизонтальной асимптоты - нет
5. Исследование на чётность.
Y(-x) ≠ - Y(x)
Функция ни чётная ни нечетная - общего вида..
6. Производная функции.
Y'(x)= 3*x² + 6*x = 3*x*(x+2) = 0
7. Корень при Х= - 2.
Возрастает - Х∈(-∞;-2)∪(0;+∞)
максимум - Y(-2) =0
минимум - Y(0) = - 4
Убывает - X∈(-2;0)
8. Вторая производная
Y"(x) = 6*x +6 = 6*(x+1)
9. Точка перегиба
Y"(x)=0 при X=-1
Выпуклая - Х∈(-∞;-1] Вогнутая - Х∈[-1;+∞).
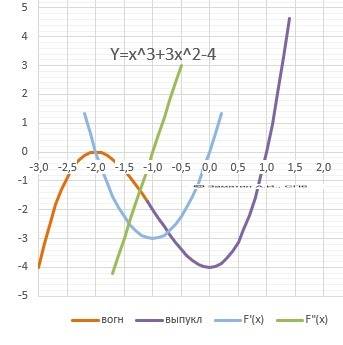
10. График в приложении.
Поскольку парабола и прямая имеют общую точку пересечения, то приравняю эти два равенства:
6x+b = x² + 8
x²-6x+8-b=0
Поскольку прямая должна касаться параболы,(то есть они имеют ровно одну общую точку), то данное квадратное уравнение должно иметь один корень(одну абсциссу точки касания, так как точка у нас одна). А такое возможно лишь при условии, что дискриминант данного уравения равен 0. Выделим сначала дискриминант из данного квадратного уравнения:
a = 1;b = -6;c = 8-b
D = b²-4ac = 36 - 4(8-b) = 36 - 32 + 4b = 4 + 4b.
D = 0
4+4b = 0
4b = -4
b = -1
Значит, при b = -1 прямая касается параболы.