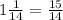
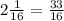
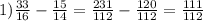
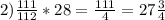
Объяснение:
Удаляем знак модуля и превращаем в квадратное уравнение: y =2*x²- 9*x- 5 ≥ 0 - квадратное уравнение.
D = b² - 4*a*c = (-9)² - 4*(2)*(-5) = 121 - дискриминант. √D = 11.
x₁ = (-b+√D)/(2*a) = (9+11)/(2*2) = 20/4 = 5 - первый корень
x₂ = (-b-√D)/(2*a) = (9-11)/(2*2) = -2/4 = -0,5 - второй корень
Это две точки где границы уравнения задачи. Записываем неравенство:
y ≥ 20 при х ∈(-∞;- 0.5]∪[5;+∞)
Наименьшее положительное - х = 5 - ответ.
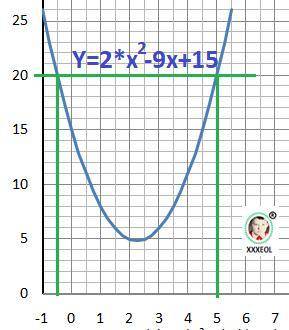
Рисунок с графиком функции показывает, что отрицательным это выражение не бывает.
Объяснение:
Удаляем знак модуля и превращаем в квадратное уравнение: y =2*x²- 9*x- 5 ≥ 0 - квадратное уравнение.
D = b² - 4*a*c = (-9)² - 4*(2)*(-5) = 121 - дискриминант. √D = 11.
x₁ = (-b+√D)/(2*a) = (9+11)/(2*2) = 20/4 = 5 - первый корень
x₂ = (-b-√D)/(2*a) = (9-11)/(2*2) = -2/4 = -0,5 - второй корень
Это две точки где границы уравнения задачи. Записываем неравенство:
y ≥ 20 при х ∈(-∞;- 0.5]∪[5;+∞)
Наименьшее положительное - х = 5 - ответ.
Рисунок с графиком функции показывает, что отрицательным это выражение не бывает.

1). (2 1/16 - 1 1/14)·28 = 56 28/16 - 28 28/14 = 57 12/16 - 30 = 27 3/4: Умножаем каждое число выражения в скобках на 28, причем отдельно умножаем целые и дробные части чисел и проводим вычитание: Это удобно, т. к. вторая дробь при умножении становится целым числом.
2). ( 33/16 - 15/14)·28 = (33·28)/16 - (15·28)/14 = (33·7)/4 -(15·28)/14 = 231/4 - 30 = 57 3/4 - 30 = 27 3/4
Переводим смешанную дробь в неправильную, затем умножаем числитель каждой дроби на 28, затем переводим первое число в смешанную дробь и вычитаем. Тоже удобно, раз знаменатель второй дроби кратен множителю.
3) (2 1/16 - 1 1/14)·28 = [(33·7)/(16·7) - (15·8)/(14·8)]·28 =[(33·7 - 15·8)/(16·7)]·28 = [(231-120)/(16·7)] ·28 = [11/(16·7)]·28 = (111·28)/(16·7)= 111/4 = 27 3/4.
Много возни с приведением к общему знаменателю