Question

Решите уравнение. |cosx+sinx|=sqrt(2)*sin2x !

Answer 1

Правая часть уравнения должна быть неотрицательной:

$sin2x \geq 0$

$2\pi k \leq 2x \leq \pi+2\pi k;k \in Z$

$\pi k \leq x \leq \frac{\pi}{2}+\pi k;k \in Z$

То есть первая и третья четверти,где синус и косинус одного знака.

Очевидно,что модуль их суммы будет больше единицы всегда(неравенство треугольника,где в качестве третьей стороны выступает радиус единичной окружности)

Рассмотрим выражение под модулем:

$cosx+sinx$

Попробуем найти максимум такой функции

$cos^2x+sin^2x=1$

$cos^2x+2sinxcosx+sin^2x=1+2sinxcosx$

$(cosx+sinx)^2=1+sin2x$

Очевидно,что левая часть принимает наибольшее значение,когда таковое принимает правая.

Правая часть принимает наибольшее значение при

$sin2x=1$

$x=\frac{\pi}{4}+\pi k,k \in Z$

$max|cosx+sinx|=\sqrt{2}$

$max(\sqrt{2}sin2x})=\sqrt{2}$

Разделим обе части уравнения на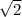 $\sqrt{2}$

$|\frac{\sqrt{2}}{2}cosx+\frac{\sqrt{2}}{2}sinx|=sin2x$

$|sin(x+\frac{\pi}{4})|=sin2x$

Очевидно,что синус в первой четверти(для третьей аналогично,так как модуль) больше тогда,когда больше аргумент.

Рассмотрим аргументы обоих синусов на полуинтервале:

$x \in [0;\frac{\pi}{4})$

$x+\frac{\pi}{4}x+x$

Значит:$|sin(x+\frac{\pi}{4})|sin2x$

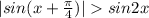
Рассмотрим аргументы обоих синусов на полуинтервале:

На этом промежутке происходит переход во вторую четверть,где с точностью до наоборот синус большего аргумента имеет меньшее значение.

$x \in (\frac{\pi}{4};\frac{\pi}{2}]$

$x+\frac{\pi}{4}<x+x$

Значит:$|sin(x+\frac{\pi}{4})|sin2x$

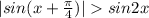
Очевидно,что единственным решением уравнения является:

$x=\frac{\pi}{4}+\pi k,k \in Z$