 ;
;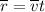 ;
;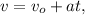 либо в векторном виде:
либо в векторном виде: 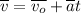 ;
;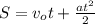 либо в векторном виде:
либо в векторном виде: 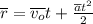 ;
;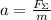 либо в векторном виде:
либо в векторном виде: 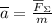 ;
; ;
;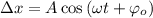 ;
;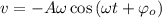 ;
; ;
;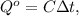 где
где 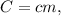 либо в удельном виде:
либо в удельном виде:  ;
;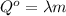 ;
;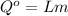 ;
; ;
; ;
;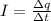 ;
;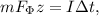 где
где  ;
;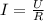 ;
;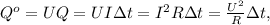
 ;
;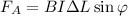 ;
; ;
;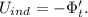
пусть 204 детали второй рабочий делает за время t;t>0
тогда первый 204 детали делает за (t-5)
производительность второго w2=204/t
производительность первого w1=204/(t-5)
за 1 час
первый сделает 1час * 204/(t-5) =204/(t-5) деталей
второй сделает 1час * 204/t =204/t деталей
по условию разница 5 детали
составим уравнение
204/(t-5) - 204/t =5
204(1/(t-5)-1/t)=5
204*(t-(t-5))/(t-5)t=5
1020 /(t-5)t =5
1020 =5(t-5)t
1020=t^2-5t
t^2-5t-1020=0
t1=-12 -по условию не подходит t>0
t2=17 час
производительность второго
w2=204/t=204/17= 12 дет - это количество деталей за 1 час
ответ 12 дет
Нельзя!
Доказательство:
Число 1 не может быть поставлено в середину ребра куба, т.к. полусумма ни одной пары оставшихся чисел не может быть равна 1. Наименьшее возможное значение такой полусуммы (2+4):2=3.
Следовательно, число 1 должно располагаться в вершине куба. Из этого вытекает, что в вершинах куба могут располагаться только нечетные числа (По условию сумма чисел, стоящих на концах ребра, должна делиться на 2 без остатка, т.е. быть четной. А сумма двух чисел, одно из которых нечетное, может быть четной только при условии, что и второе число тоже нечетное).
Из этого следует, что число 20 будет располагаться в середине какого-либо ребра куба. Очевидно, что число 20 не может быть полусуммой каких-либо двух чисел, каждое из которых меньше 20.
Вывод: расположить числа указанным в задаче невозможно.