3х+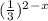 ≥10
≥10
обследуем,как ведет себя функция на промежутке -∞;0
видно,что левая часть всегда отрицательная,тк как дробь стремится к нулю
значит наше число положительное
если х=0,то левая часть <10
х=1-----------------<10
х=2 <10
х=3 >10
значит наименьшее целое число,удовлетворяющее неравенству равно 3
ответ:f(x) возрастает на (-∞;-5) ∪ (8;+∞), f(x) убывает на (-5;8)
Объяснение:1)найдём ОДЗ: х∈R;
2) f'(x)= 6x²-18x-240
3) найдём критические точки, для чего приравняем производную к нулю: f'(x)=0, если 6x²-18x-240=0 ⇒x²-3x-40=0 ⇒ дискриминант D= 9+160=169=13² ⇒ x₁=(3+13)/2=8, x₂=(3-13)/2= -5, т.е. x₁=8, x₂= -5 - критические точки
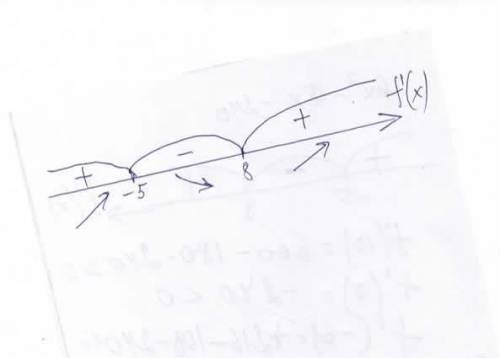
4) Отметим критические точки на координатной прямой, они разбивают её на 3 интервала (выполнить рисунок): (-∞;-5), (-5;8), (8;+∞). Найдём знак производной в каждом из этих интервалов:
на (-∞;-5) f'(x)>0;
на (-5;8) f'(x)<0;
на (8;+∞) f(x)>0
если производная функции y=f(x) положительна для любого x из интервала (a;b), то функция возрастает на (a;b);
если производная функции y=f(x) отрицательна для любого x из интервала (a;b) , то функция убывает на (a;b) .
Значит f(x) возрастает на (-∞;-5) ∪ (8;+∞), f(x) убывает на (-5;8)
Пусть х км\ч - скорость лодки в неподвижной воде
х+10- скорость по течению реки
х-10 - скорость против течения реки
время, затраченное на путь против течения: 91/х-10
время, затраченное на путь по течению: 91/х+10
По условию сказано, что на обратный путь было затрачено на 6 часов меньше.
Составим и решим уравнение.
91/х-10= 91/х+10+ 6
91(х+10) = 91(х-10) + 6(х+10)(х-10)
91х+910=91х-910+6х^2-600
6х^2-600=0
x^2-100=0
x^2=100
х=10, х=-10
-10 не подходит по условию задачи, значит скорость лодки в неподвижной воде 10 км\ч
ответ: 10 км\ч
Это либо число 2,либо какое-то дробное!С 2 вроде получается 10