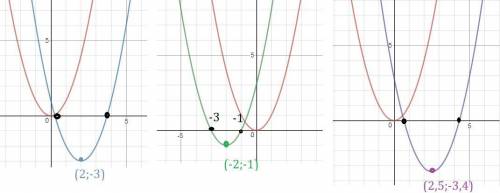
1) Шаблон y=x²
Вершина в точке (2;-3)
Нули функции
(x-2)²-3=0 ⇒
(x-2)²=3
x-2= -√3 или х-2=√3
х=2-√3 или х=2+√3
2) Шаблон y=x²
Вершина в точке (-2;-1)
Нули функции
(x+2)²-1=0 ⇒
(x+2)²=1
x+2= -1 или х+2=1
х=-3 или х=-1
3) Шаблон y=x²
Вершина в точке (2,5;-3,4)
Нули функции
(x-2,5)²-3,4=0 ⇒
(x-2,5)²=3,4
x-2,5= -√3,4 или x-2,5=√3,4
х= 2,5 -√3,4 или х=2,5 +√3,4
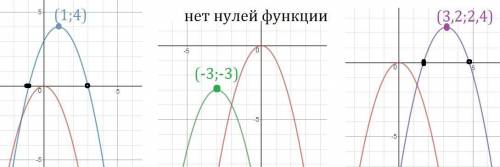
4)Шаблон y= - x²
Вершина в точке (1;4)
Нули функции
-(x-1)²+4=0 ⇒
(x-1)²=4
x-1= -2 или x-1=2
х= -1 или х=3
5)Шаблон y= - x²
Вершина в точке (-3;-3)
Нули функции
-(x+3)²-3=0 ⇒
(x+3)²=-3
уравнение не имеет корней.
Парабола не пересекает ось Ох
6)Шаблон y= - x²
Вершина в точке (3,2;2,4)
Нули функции
-(x-3,2)²+2,4=0 ⇒
(x-3,2)²=2,4
x-3,2= - √2,4 или x-3,2= √2,4
x= 3,2 - √2,4 или x = 3,2+ √2,4
Объяснение:
{ x² - y² = 4 , ⇒ { x² - y² = 4 , ⇒ { x² - y² = 4 , ⇒
{ x⁴ - y⁴ = 64 ; { (x² - y²)(x² + y²) = 64 ; { 4(x²+ y²) = 64 ;
{ x² - y² = 4 ,
{ x²+ y² = 16 ; додаємо рівняння системи :
2x² = 20 ; > x² = 10 ; > x₁,₂ = ± √10 . При таких
значеннях х із ІІ - го рівняння останньої системи маємо :
10 + у² = 16 ; > у² = 16 - 10 ; > у² = 6 ; > y₁,₂ = ± √6 .
Отже , x²+ y² = 16 ; а розв"язки системи такі :
(- √10 ;- √6 ) , (- √10 ; √6 ) , ( √10 ;- √6 ) , ( √10 ; √6 ) .
Система рівнянь має 4 розв"язки .