Алгебра: Решите неравенство x²+x-20 меньше 0, методом параболы

Решите неравенство x²+x-20 меньше 0, методом параболы

👇

Ответ:

Alesha55535

18.06.2020

Найдем корни уравнения х²+х-20=0
D = 1² - 4 * (-20) = 1 + 80 = 81 = 9²
х1 = (-1 - 9) / 2 = -5
х2 = (-1 + 9)/2 = 4
т.е. парабола пересекает ось ОХ в точках -5 и 4
коэффициент при х² положительный, значит, ветви параболы направлены вверх.
Можно построить график (см. вложенный файл) для наглядности, можно и обойтись.
График расположен ниже оси ОХ в промежутке -5 < x < 4
ответ. -5 < x < 4

4,6(73 оценок)

Открыть все ответы

Ответ:

Sasci

18.06.2020

35.

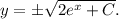
$y = \pm\sqrt{2e^x + C}.$

37.

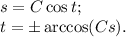
$s = C\cos t;\\t = \pm\arccos (Cs).$

39.

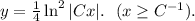
$y = \frac14 \ln^2 |Cx|.\ \ (x \geq C^{-1}).$

Объяснение:

35.

Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. В исходном случае переменные уже разделены, поэтому можно непосредственно проинтегрировать обе части уравнения:

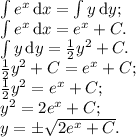
$\int e^x \, \text{d}x = \int y \, \text{d}y;\\\int e^x\, \text{d}x = e^x + C.\\\int y\, \text{d}y = \frac12 y^2 + C.\\\frac12 y^2 + C = e^x + C;\\\frac12 y^2 = e^x + C;\\y^2 = 2e^x + C;\\y = \pm\sqrt{2e^x + C}.$

ответом будет являться найденная функция .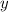

37.

Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. Разделим переменные:

$\text{tg}\, t\, \text{d}t = - \frac{\text{d}s}{s}.$

Теперь можно непосредственно проинтегрировать обе части уравнения:

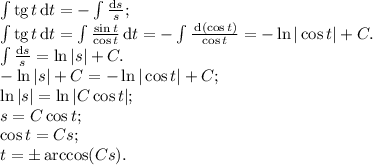
$\int \text{tg}\,t \, \text{d}t = - \int \frac{\text{d}s}{s};\\\int \text{tg}\,t \, \text{d}t = \int \frac{\sin t}{\cos t} \, \text{d}t = - \int \frac{\, \text{d}(\cos t)}{\cos t} = -\ln |\cos t| + C.\\\int \frac{\text{d}s}{s} = \ln |s| + C.\\-\ln |s| + C = -\ln |\cos t| + C;\\\ln |s| = \ln |C\cos t|;\\s = C\cos t;\\\cos t = Cs;\\t = \pm\arccos (Cs).$

Не знаю, что здесь функция, а что переменная, так что в ответе будут в явном виде и s, как если бы переменной была t, и t, как если бы переменной была s.

39.

Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. Разделим переменные:

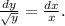
$\frac{dy}{\sqrt y} = \frac{dx}{x}.$

Теперь можно непосредственно проинтегрировать обе части уравнения:

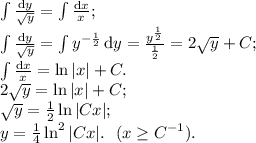
$\int \frac{\text{d}y}{\sqrt y} = \int \frac{\text{d}x}{x};\\\int \frac{\text{d}y}{\sqrt y} = \int y^{-\frac12}\, \text{d}y = \frac{y^\frac12}{\frac12} = 2\sqrt y + C;\\\int \frac{\text{d}x}{x} = \ln|x| + C.\\2\sqrt y = \ln |x| + C;\\\sqrt y = \frac12 \ln|Cx|;\\y = \frac14 \ln^2 |Cx|.\ \ (x \geq C^{-1}).$

ответом будет являться найденная функция 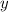с условием.

4,4(89 оценок)

Ответ:

Maksim9999v

18.06.2020

Объяснение:

1) Kl=12; KM:ML= 3 : 1

KM=3ML

KM+ML=KL

3ML+ML=12

4ML=12

ML=3

KM=3ML=9

2) AB/ED=YX/LK; AB= 2 см, ED= 3 см и LK= 27 см

YX=LK·AB/ED=27·2/3=54/3=18

YX=18 см

3) ΔKBC∼ΔRTG; k= 18; P₁=8; S₁=9; P₂=?, S₂=?

Условие не полное. Не определена зависимость сторон от коэффициента подобия к. То есть какие стороны подобны(это не обязательно), а главное порядок отношения сторон относительно к.

Рассмотрю оба случая:

a) ΔKBC∼ΔRTG⇒P₂/P₁=k; S₂/S₁=k²

P₂=kP₁=8·18=144 см

S₂=k²S₁=8²·9=64·9=576 см²

б) ΔKBC∼ΔRTG⇒P₁/P₂=k; S₁/S₂=k²

P₂=P₁/=18/8=2,25 см

S₂=S₁/k²=9/8²=9/64 см²

4,6(70 оценок)

Это интересно:

Компьютеры-и-электроника

31.05.2022

Как сделать полный сброс на телефоне Nokia N73...