Стандартный с рассмотрением различных случаев раскрытия модулей давно надоел. Есть очевидный, использующий геометрический смысл модуля (модуль разности чисел равен расстоянию между ними, поэтому |x| - это расстояние от x до нуля, |x+4| - расстояние от x до минус четырех. Ясно что сумма расстояний равна 12, когда x = 4 и x = - 8, а меньше 12 - когда мы находимся слева от 4 и справа от - 8. Во второй задаче подобные рассуждения приводят к тому, что решений нет.)
Но мы пойдем другим путем, который мне подсказал Голубев В.И. своими статьями в газете Математика, а затем своей книгой "Решение сложных и нестандартных задач по математике". Каждый желающий может посмотреть эту книгу - она есть в электронном виде, я же здесь буду применять метод без объяснений.
1) ![|x|+|x+4|\le 12\Leftrightarrow\left\{\begin{array}{c} x+(x+4)\le 12\\ x-(x+4)\le 12\\ -x+(x+4)\le 12\\ -x-(x+4)\le 12\end{array}\right.\Leftrightarrow\left\{\begin{array}{c} x\le 4\\ -4\le 12\\ 4\le 12\\ x\ge -8\end{array}\right.\Leftrightarrow x\in [-8;4].](/tpl/images/1873/9672/df404.png)
2) 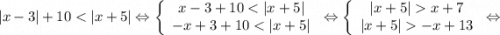

Нужно взять во внимание два условия.
(1) Подкоренное выражение должно быть неотрицательным.
(2) Знаменатель дроби не должен быть равен нулю.
Учитывая их, записываем следующую систему.
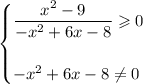
Для начала решим отдельно верхнее неравенство системы. Его можно решить методом интервалов, предварительно разложив на множители числитель и знаменатель.
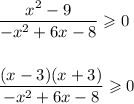
Числитель мы разложили по формуле сокращённого умножения (разность квадратов). Для разложения знаменателя понадобится найти корни следующего уравнения:
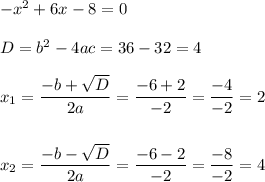
Используя следующую формулу: 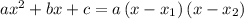 , где
, где 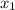 и
и 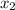 - корни уравнения
- корни уравнения 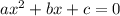 , получаем:
, получаем: 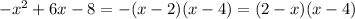 , здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
, здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
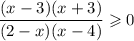
Решим данное неравенство методом интервалов.
Нули числителя: -3; 3.
Нули знаменателя: 2; 4.
- + - + -
----------------- -----------------о-----------------
-----------------о----------------- -----------------о-----------------> x
-----------------о-----------------> x
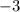
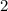
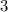
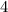
Так как знак в последней строке неравенства "больше или равно", то подходят те промежутки, где стоит знак "плюс". В нашем случае: 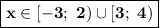 .
.
Решением нижнего выражения являются 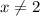 и
и 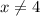 . В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
. В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
ответ: 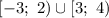 .
.
2c+2k-c²-ck=2(c+k)-c(c+k)=(2-c)(c+k)
3c+3k-2c²-2ck=3(c+k)-2c(c+k)=(3-2c)(c+k)