Дано неравенство: х/(х^2+7x+12)< x/(x^2+3x+2).
Разложим знаменатели заданных дробей на множители.
х^2+7x+12 = 0, Д = 49-48=1, х1,2 = (-7+-1)/2 = -3 и -4.
x^2+3x+2 = 0, Д = 9-8 = 1, х1,2 = (-3+-1)/2 = -1 и -2.
Заданное неравенство можно представить так:
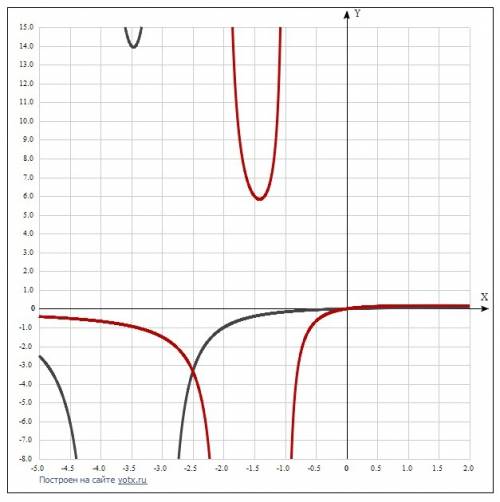
х/((х+3)(х+4) < х/((х+1)(х+2).
Отсюда получаем 4 точки разрыва функции : х = -4, -3, -2 и -1.
Находим абсциссу равенства двух дробей. Числители равны - приравняем знаменатели: х^2+7x+12 = x^2+3x+2, 4х = -10, х = -2,5.
Используя метод интервалов определяем промежутки, на которых выполняется заданное условие неравности.
ответ: x > 0; -3 < x < -2,5; -2 < x < -1; x <-4.
ответ: нет
Решение: По свойству остаток от деления на натуральное число m разницу натуральных чисел a и b, равен разнице остатков от деления a/m - b/m или r1 - r2;
Найдём r1
Для определения остатка при деление на 5 нам достаточно знать последнюю цифру.
У числа 77777 последней цифрой может быть 7, 49, 63, 1
а далее снова идут 7 49 63 1
Таким образом через каждый 4 возведения в степень мы получаем остаток 7, тогда раз 2015 / 4 = 503 + 3/4, то получается у нас 503 раза повторятся остатки 7 49 63 1, а дальше 7 49 63
Таким образом r1 = 63/5 == 3 (то есть остаток = 3)
Аналогично найдём остаток r2
33333^2015 опять же найдём все последние цифры;
Ими будут 3 9 7 1 3 9 7 1, то есть опять каждые 4 возведения в степень мы получаем повтор остатков. => 503 у нас повторится 3 9 7 1
А уже у числа 33333^2012 == 1 33333^2013 == 3
33333^2014 == 9 33333^2015 == 7 (== указание последней цифры числа)
Таким образом r2 = 7/5 == 2 (то есть остаток равен 2)
r1 - r2 = 3 - 2 = 1
Таким образом, разность данных чисел не делится на 5