Дано:
b(n) - геометрическая прогрессия;
b₄ = 8;
b₇ = 512
1) Найти q.
2) Найти n при S(n)=2 ⁵/₈
Решение.
1) Воспользуемся формулой общего члена геометрической прогрессии: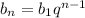 
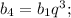
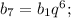
Подставим b₄ = 8; и b₇ = 512 и получим:
;
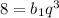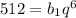
Второе уравнение преобразуем:
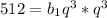
Подставим из первого уравнения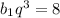 
во второе и получим:
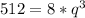
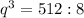
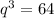
![q=\sqrt[3]{64}](/tpl/images/3193/8714/c03df.png)
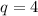
2) Найдем b₁ с первого уравнения:
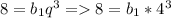
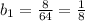
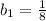
3)Воспользуемся формулой суммы первых членов геометрической прогрессии:
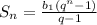
Подставим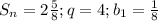 
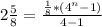
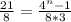
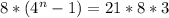
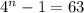
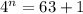
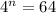
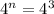
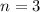
3 перших члена прогресії потрібно взяти, щоб їхня сума дорівнювала
2 ⁵/₈
ответ: 1) q=4;
2) n=3
Проверка:
¹/₈ + ⁴/₈ + ¹⁶/₈ = ²¹/₈ = 2 ⁵/₈
m = - b/(2a)
m = 6/2 = 3
n = 3² - 6*3 + 11 = 2
(3;2) - точка минимума функции