1)Координаты вершины параболы (0,25; -3,125)
2)Прямая у=х-2 пересекает параболу у= -х²+4 в двух точках.
Координаты точек пересечения (-3; -5) (2; 0)
3)График функции
Объяснение:
1)Найти координаты вершины параболы
у=2х²-х-3
х₀= -b/2a= 1/4=0,25
у₀=2*0,25²-0,25-3=0,125-0,25-3= -3,125
Координаты вершины параболы (0,25; -3,125)
2)Найти координаты точек пересечения графиков функций
у= -х²+4 и у=х-2 без построения.
Нужно приравнять правые части уравнений (левые равны):
-х²+4 = х-2
-х²+4-х+2=0
-х²-х+6=0
х²+х-6=0, квадратное уравнение, ищем корни:
х₁,₂=(-1±√1+24)2
х₁,₂=(-1±√25)2
х₁,₂=(-1±5)2
х₁= -6/2= -3 у₁=х₁ -2= -3-2= -5
х₂=4/2=2 у₂=х₂ -2= 2-2=0
Прямая у=х-2 пересекает параболу у= -х²+4 в двух точках.
Координаты точек пересечения (-3; -5) (2; 0)
3)Построить график функции у=5-х²
Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
у= -х²+5
График парабола, ветви направлены вниз, координаты вершины
(0; 5)
Таблица
х -4 -3 -2 -1 0 1 2 3 4
у -11 -4 1 4 5 4 1 -4 -11
Объяснение:
2.
a) 3x+12>4x-1 | (-x>-13) /-1 | x<13
7-2x<=10-3x | -3 <= -x /-1 | x <= 13. x принадлежит (-∞; 13].
б) 2x-9 > 6x+1 | (-4x > 10) / -4 | x<10
( -
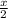< 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
3.
а)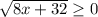 
Взводим все в квадрат
8x+32 => 0
8x => 32 делим все на 8
x => 4. x принадлежит [4; +∞).
б)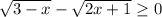 
Взводим все в квадрат
3-x-2x+1 => 0
4 => 3x Делим все на 3
1.3 => x
x <= 1.3. x принадлежит [-∞; 1.3).
4.
а-7 => 0 3-2a => 0
a => 7 3 => 2a
1.5 => a ответ: a принадлежит [7; +∞).
пусть х - проехал до встречи автобус
тогда (0,5 + х)- проехал мотоциклист (0,5 - это полчаса)
60*(0,5+х)- путь, проделанный мотоциклистом
50*х - путь проделанный автобусом
Зная, что весь путь = 195 км, составим уравнение
60*(0,5+х)+50*х=195
30+60*х+50*х=195
110*х=195-30
110*х=165
х=165/110
х=1,5 часа проехал до встречи автобус