Постройте график функции,выбрав соответствующий масштаб:
а)y=100x
для того чтобы построить график функции ( а графиком будет прямая)
напишем таблицу значений
х 1 2
у 100 200
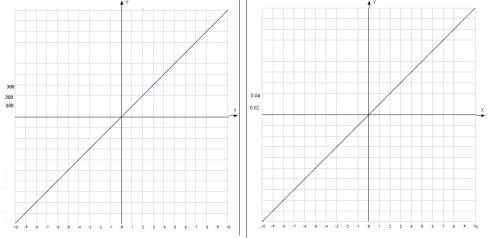
Видим что изобразить точки с координатами (1;100) и (2;200) в тетради не получится, нам придется поменять масштаб
Это значит по оси Ох каждую клеточку обозначим за 1
а по оси Оу каждую клеточку обозначим например за 100 еденичных отрезков
и теперь отмечам точки.
получится точка (1;100) : 1 клеточка по оси Ох и 1 клеточка по оси Оу
б) y=0,02x
рассуждаем так же
х 1 2
у 0,02 0,04
тут ситуация наоборот. Слишком маленькие значения для у
тогда придется увеличить масштаб
по оси Ох 1 клеточка за 1
по оси Оу 1 клеточка за 0,02
Объяснение:
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Доказательство делимости и кратности
Доказательство равенств и тождеств
Задачи с последовательностями
Доказательство неравенств
Нахождение суммы и произведения
y(-x)=-5x^3+x=-(5x^3-x)=-y(x) нечетная
y(-x)=2(-x)^8/-(-x)^3=2x^8/x^3=-2x^8/-x^3=-y(x) - нечетная