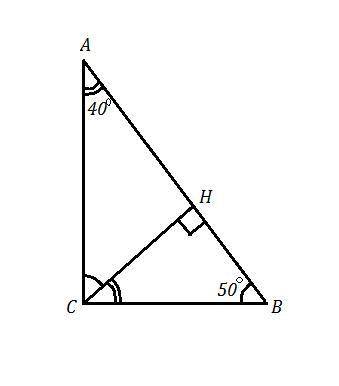
ΔАВС , ∠С=90° , ∠В=50° ⇒ ∠А=90°-∠В=90°-50°=40°
СН ⊥ АВ ⇒ ∠СНА=90° и ∠СРВ=90° .
Рассм. ΔВСН . Он прямоугольный и ∠В=50° , тогда ∠ВСН=90°-50°=40°. Это угол, образованный высотой СН с меньшим катетом (катет ВС лежит против меньшего острого угла ΔАВС).
Рассм. ΔАСН . Он прямоугольный и ∠А=40° , тогда ∠АСН=90°-40°=50°. Это угол, образованный высотой СН с бОльшим катетом АС (катет АС лежит против бОльшего острого угла ΔАВС).
Замечание. Так как у треугольников ΔАВС , ΔВСН и ΔАСН все три угла равны, то эти треугольники подобны .
1) x+3y+2z=37 ×(-2/1) ×(-3/1) 2) x+3y+2z=37
2x+y+z=22 (-2x)-6y-4z+2x+y+z=(-74)+22
3x+2y+2z=42 (-3x)-9y-6z+3x+2y+2z=-(111)+42
3) x+3y+2z=37 4) x+3y+2z=37
(-5y)-3z=(-52) *(-1.4) (-5y)-3z=(-52)
(-7y)-4z=(-69) (-7y)-4z+7y+4.2z=72,8-89
5) x+3y+2z=37 6)z=19
(-5y)-3z=(-52) (-5y)-3*19=52⇒ (-5y)=109⇒y=(-21.8)
0.2z=3.8 x+3*(-21.8)+2*19=37⇒x=64.4
Объяснение: чтобы избавиться от корней мы прибавляем первое уравнение ко второму и третьему изначально использовав отношение первого неизвестного второго уравнения на первое с отрицательным знаком. Немудрено понять что в итоге 2/1 это два только с противоположным знаком. Перемножаем и прибавляем ко второму. Так же нужно поступить с третьим уравнением взяв отношение 3 к 1 с противоположным знаком соответственно.
Избавляемся в обоих уравнениях от первого неизвестного, следующим шагом берем отношение второго неизвестного второго уравнения и второго неизвестного третьего и получаем -7/-5 c противоположным знаком. Избавляемся от второго неизвестного и получаем обыкновенное уравнение
Следующие действия совершаются методом подстановки и решением простейшего уравнения.