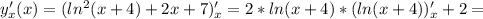
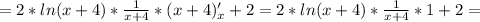
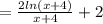
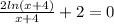
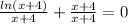
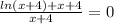
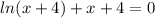
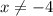 для него сохраняется.
для него сохраняется.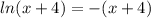
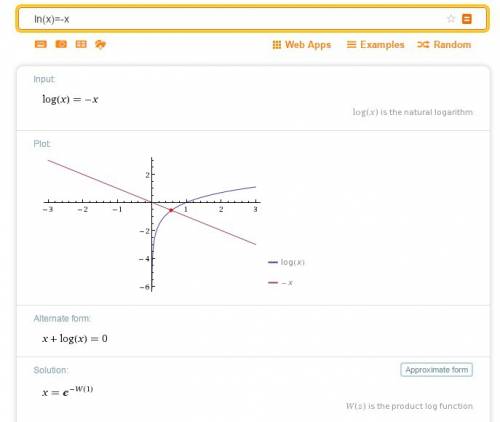
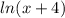 монотонно растет, функция же
монотонно растет, функция же 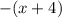 монотонно убывает, что означает, что у уравнения существует лишь один корень.
монотонно убывает, что означает, что у уравнения существует лишь один корень.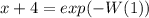
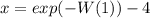
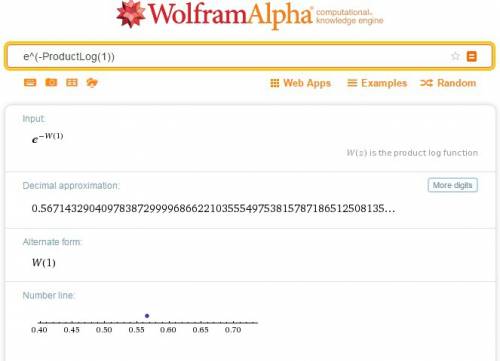
 в бесконечность, действительные значения исследуемой функции также тогда устремятся в бесконечность:
в бесконечность, действительные значения исследуемой функции также тогда устремятся в бесконечность: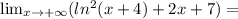
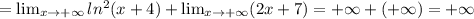
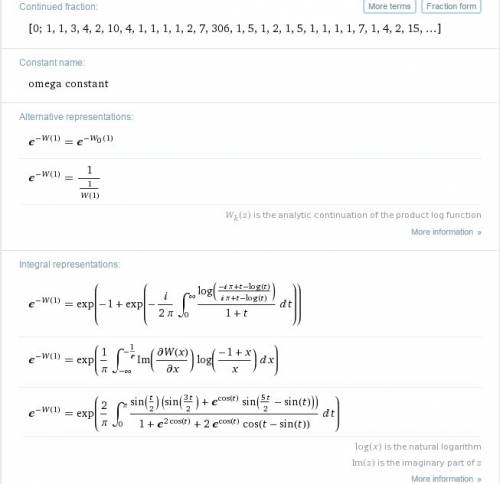
 , она непрерывно растет.
, она непрерывно растет.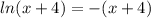
x²-3x-10
Разложим все на множители:
x²-9x+20=0
D=81-80=1
x₁=9-1=4
2
x₂=9+1=5
2
x²-9x+20=(x-4)(x-5)
x²+3x+2=0
D=9-8=1
x₁=-3-1=-2
2
x₂=-3+1=-1
2
x²+3x+2=(x+2)(x+1)
x²-3x-10=0
D=9+4*10=49
x₁=3-7=-2
2
x₂=3+7=5
2
x²-3x-10=(x+2)(x-5)
y=(x-4)(x-5)(x+2)(x+1) = (x-4)(x+1)=x²-4x+x-4=x²-3x-4
(x+2)(x+5)
y=x²-3x-4
Парабола, ветви вверх.
1) Вершина параболы:
х₀=-b = -(-3)=1.5
2a 2
y₀=(1.5)²-3*1.5-4=6.25
(1.5; 6,25) - вершина параболы
2) х=1,5 - ось симметрии
3) Нули функции:
x²-3x-4=0
D=9+16=25
x₁=3-5=-1
2
x₂=3+5=4
2
4) Точки для построения:
x| -3 | -2 | -1 | 0 | 1 | 1.5 | 2 | 3 | 4 | 5 | 6
y| 14| 6 | 0 | -4| -6| -6.25 | -6 | -4 | 0 | 6 | 14
y=-6.25 имеет одну общую точку с заданной функцией.
ответ: -6,25