Иногда называют тождеством также равенство, не содержащее никаких переменных; напр. {\displaystyle 25^{2}=625.}
Не любое равенство является тождеством. Например, равенство {\displaystyle x+2=5} имеет место не при всяком значении {\displaystyle x}, а только при {\displaystyle x=3}. Поэтому оно не является тождеством. Кроме того, равенство может выполняться, например, при положительных значениях переменных и не выполняться (или не иметь смысла) при отрицательных, см. об этом следующий раздел.
Тождественное равенство, когда его хотят подчеркнуть особо, обозначается вместо знака равенства символом «≡».
Данное уравнение не имеет целых корней.
Используем метод Феррари:
уравнение вида
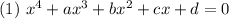
с замены 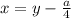
приводим к виду:
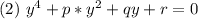
где:
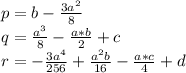
добавим и вычтем из левой части уравнения 2 выражение 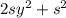 , где s - некоторое число:
, где s - некоторое число:

получим:
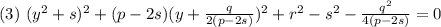
Пусть s - корень уравнения
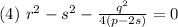
Тогда уравнение 3 примет вид:
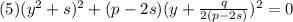
Избавляемся в уравнении 4 от знаменателя:
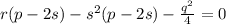
Раскроем скобки и получим:
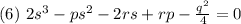
Уравнение 6 называется кубической резольвентой уравнения 4 степени.
Разложим уравнение 5 на множители:
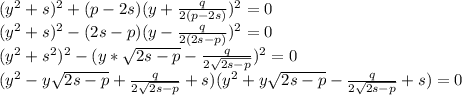
Получим два квадратных уравнения:
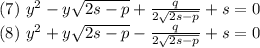
Применяем этот метод для решения уравнения
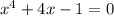
Перепишем уравнение в полном виде:
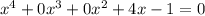
коэффиценты:
a=0
b=0
c=4
d=-1
определяем p,q и r:
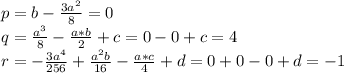
ищем s:
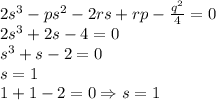
подставляем p,q,r и s в квадратные уравнения 7 и 8:
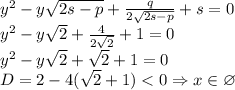
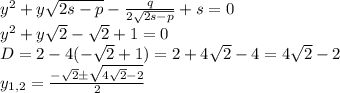
Теперь находим x:
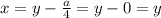
ответ: 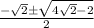
{-5=k*(-3)+b {-5=-3k+b
1=k*1+b b=1-k
-5=-3k+1-k
4k=6, k=1,5
b=1-1,5. b=-0,5
y=1,5x-0,5