№1
а) √50 > 7
√50 > √7²
√50 > √49
б) 4√6 > 3√7
√4²*6 > √3²*7
√16*6 > √9*7
√96 > √63
№2
а) √(196 * 0,64) = √(14²*(0,8)²) = 14 * 0,8 = 11,2
б) √(72*0,5)=√36=√6² = 6
в) 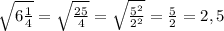
г) √(-2)⁶ = √((-2)³)²=(-2)³= - 8
№3
а) (√3+√2)² = (√3)²+ 2 *√3*√2 + (√2)²= 3 + 2√6 + 2 = 5 +2√6
б) (4 - √5)(4 + √5) = 4² - (√5)² = 16 - 5 = 11
в) 5√12 - 2√27 - 3√3 = 5√(4*3) - 2√(9*3) - 3√3 = 5√(2²*3) - 2√(3²*3) - 3√3 = 5*2√3 - 2*3√3 - 3√3= 10√3 - 6√3 - 3√3 = √3
№4
√(72*а⁵) = √(36*2 * а⁴*а)= √(6²*2 * (а²)² * а) = 6*а²*√(2а)
№5
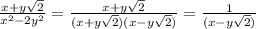
№6
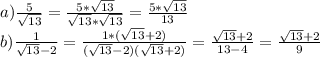
63
Объяснение:
Пусть первая цифра двузначного числа (т.е. число его десятков) равна а, тогда сумма цифр этого двузначного числа равна а+3.
Двузначное число, записанное теми же цифрами, но в обратном порядке запишем поразрядно: 10*3+а
Т.к. по условию, сумма цифр двузначного числа, умноженная на 4 равна двузначному числу, в котором цифры данного двузначного числа записаны в обратном порядке, то можно составить уравнение:
4(a+3) = 10*3+a
4a+12 = 30+a
4a-a = 30-12
3a = 18
a = 18:3
a = 6
63 - искомое двузначное число
16-8x<15-9x+27
9x-8x<26
x<26
x∈(-∞;26)