Объяснение:
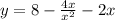
На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)
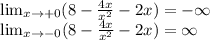
Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.
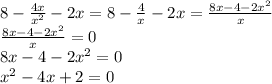
Решаем квадратное уравнение, находим точки пересечения с осью х:
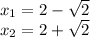
Находим точки экстремума (производная равна нулю).
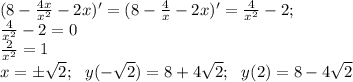
Для нахождения точек перегиба находим вторую производную
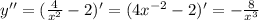
Вторая производная нигде не равна нулю, точек перегиба нет.
Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.
Ищем наклонную асимптоту:
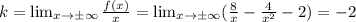
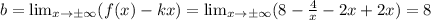
Наклонная асимптота есть:
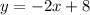
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).
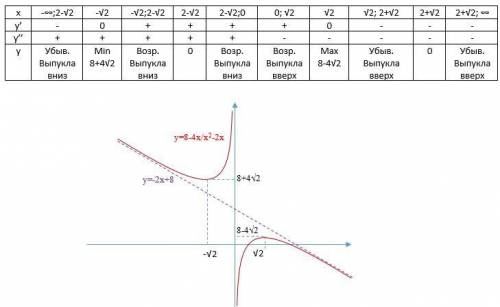
f(x)=x²-3x+2
Найдём нули функции:
х²-3х+2=0
х²-х-2х+2=0
х(х-1)-2(х-1)=0
(х-2)(х-1)=0
х-2=0 => x=2
x-1=0 => x=1
Точки пересечения параболы с осью Х: (1;0) и (2;0)
Найдем вершину параболы по формуле x=-b/2a: a=1; b=-3: x=3/2*1=1.5
y=1.5²-3*1.5+2
y=-0.25
Координаты вершины параболы: (1.5;-0.25)
Все. Параболу можно построить по этим 3-м точкам: (1;0), (1.5;-0.25) и (2;0).
Чтобы график был точнее, можно найти еще несколько точек, подставляя различные значения х в уравнение параболы.
Таблица и график во вложении

2 * (v-2) + 1,5 *2 = 35
2*v - 4 + 3 = 35
2*v = 35+1
2*v = 36
v = 18
Собственная скорость лодки равна 18 км/ч