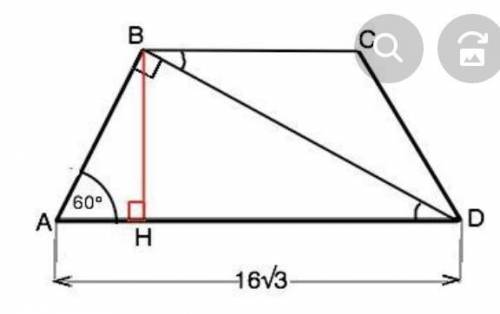
Обозначим трапецию АВСD, AB=CD, АD=16√3, ∠BAD=60°. ∠ABD=90°. Треугольник АВD- прямоугольный, ⇒ ∠АDB=180°-90°-60°=30°. Сторона АВ противолежит углу 30° и равна половине AD. АВ=8√3. Опустим высоту ВН на большее основание. Треугольник АВН - прямоугольный, ∠ АВН=180°-90°-60°=30°. Катет АН=АВ:2=4√3. ⇒ DH=AD-AH=16√3-4√3=12√3. Высота ВН=АВ•sin60°=8√3•(√3/2)=12. Высота равнобедренной трапеции, проведенная из тупого угла, дели основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности⇒ DH=(AD+BC):2. Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=BH•DH=12•12√3=144√3 (ед. площади)
==========
Как вариант решения можно доказать, что треугольник DCB - равнобедренный, ВС=CD=AB, вычислить длину высоты и затем площадь ABCD.
Пусть b1,b2,,bn, - члены прогрессии, а q - её знаменатель. Сумма прогрессии S=b1/(1-q). По условию, b1/(1-q)=6. Одновременно по условию S1=b1²+b2²++bn²+=12. Но S=b1*(1+q+q²+q³), а S1=b1²*(1+q²+q⁴+q⁶+). Получена система уравнений:
b1*(1+q+q²+q³)=6
b1²*(1+q²+q⁴+q⁶+)=12
Возведём первое уравнение в квадрат:
b1²*(1+q+q²+q³)²=36
b1²*(1+q²+q⁴+q⁶+)=12
Разделив теперь первое уравнение на второе, придём к уравнению относительно q: (1+q+q²+q³+)²/(1+q²+q⁴+q⁶+)=3. Но в скобках числителя - бесконечная геометрическая прогрессия со знаменателем q, её сумма S2=1/(1-q). В скобках знаменателя - бесконечная геометрическая прогрессия со знаменателем q², её сумма S3=1/(1-q²). Отсюда следует уравнение (1-q²)/(1-q)²=3, которое приводится к квадратному уравнению 2*q²-3*q+1=0. Решая его, находим q1=1 и q2=1/2. Но при q=1 сумма прогрессии была бы равна бесконечности, поэтому q=1/2. ответ: 1/2.
После повышения стала A₁= A +A*p₁/100 =A(1+p₁/100), здесь p₁=30% ;
(начальное значение A умноженное на коэффициент (1+p₁/100) .
после снижения A₂ =A₁+A₁*p₂/100 = A₁(1+p₂/100), здесь p₂= - 40% ;
опять нач. значение в данный момент A₁ умноженное на коэффициент (1+p₂/100).
A₂ =A₁(1+p₂/100) =A(1+p₁/100)*(1+p₂/100) .
A(n) =A((1+p₁/100)*(1+p₂/100) * (1+p(n)) , p(i) _ знаком " +" или " - " .
В частности , если p₁=p₂ =p₃= =p(n) = P ,получается :
A(n) =A(1+P/100) ^(n) .
A +A*p/100 = A(1+p₁/100)*(1+p₂/100) ;
A(1+p/100) = A(1+p₁/100)*(1+p₂/100) ;
1+p/100 = (1+p₁/100)*(1+p₂/100) *** сюда A не входит , поэтому прав был тот , который взял любую начальную цену удобную для выполнения арифметических действий ***
1+p/100 =(1+30/100)*(1 - 40/100) ⇒ p = - 22 % .
1+p/100 =1,3* 0,6 ;
1+p/100 =0,78 ;
p/100 = 0,78 -1;
p/100 = -0,22 ;
p =( - 0,22)*100 ;
p = - 22 % .