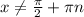
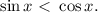
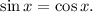Решать его можно, деля на косинус и получая при этом уравнение относительно тангенса. Но проще вспомнить, что косинус и синус - это абсцисса и ордината точки на единичной окружности. Они равны на биссектрисе 1-го и 3-го координатных углов. Меньше же ордината будет ниже этой прямой,чему соответствуют промежутки от 
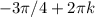до 
.
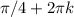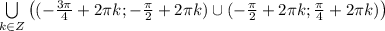
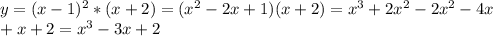
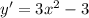
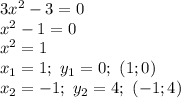
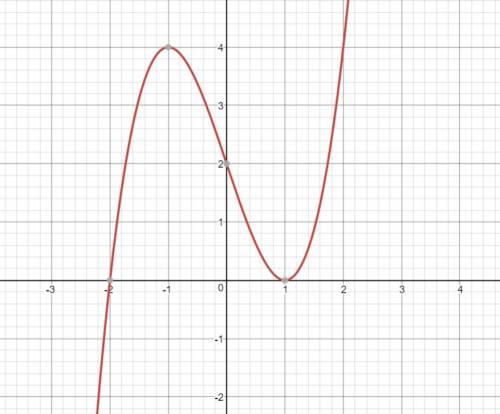
![x \in [-1;1]](/tpl/images/0855/7298/e8244.png)
- функция убывает![x \in (-\infty;-1]\cup[1;+\infty)](/tpl/images/0855/7298/459c9.png)
- функция возрастает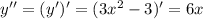
Sin x( 2Cos x + √2) - (2Cos x + √2) = 0
(2 Cos x + √2)( Sin x - 1) = 0
a) 2Cos x + √2 = 0 или б) Sin x -1=0
Cos x = -√2/2 Sin x = 1
x = +- arcCos (-√2/2) + 2πk, k∈Z x = π/2 + 2πn , n ∈Z
x = +-3π/4 + 2πk , k∈Z