Пусть х км расстояние, которое проехал велосипедист до встречи. Тогда мотоциклист проехал до встречи (80 - х) км. Так как велосипедист приехал в В через 3 часа после встречи, то он проехал расстояние (80 - х) км за 3 часа, а значит его скорость (80 - х)/3 (км/ч). Мотоциклист же расстояние х км проехал за 1 ч.20мин., т.е. за 4/3 часа, поэтому его скорость х: 4/3 = 3х/4 (км/ч). Так как до встречи они затратили одинаковое время, то можно составить уравнение:
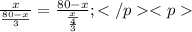
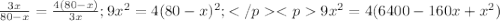
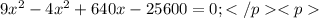
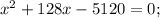
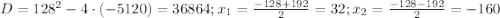
Так как за х мы брали расстояние от А до места встречи, то х = 32 (км).
ответ: На расстоянии 32 километра от пункта А произошла встреча.
Объяснение:
Имеется два существенно различных задания множеств. Можно либо перечислить все элементы множества, либо указать правило для определения того, принадлежит или не принадлежит рассматриваемому множеству любой данный объект.
Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B.
Пустое множество — множество, не содержащее ни одного элемента. Одноэлементное множество — множество, состоящее из одного элемента. Универсальное множество (универсум) — множество, содержащее все мыслимые объекты.
Пересечением двух множеств, называется третье множество, сформированное из элементов, которые входят в оба первых множества.
Объединением двух множеств A и B называется множество A B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств A или B. Пересечением множеств A и B называется множество A B, которое состоит из тех и только тех элементов, которые принадлежат как множеству A, так и множеству B.
x^2y^2(x^2 + y^2) = 468 (2)
Работаем с (1)
(х+у)(х² - ху + у²) + ху( х +у) = 13
(х + у)(х² - ху + у² +ху) = 13
(х + у)(х² + у²) = 13
(х² + у²) = 13/(х + у)
Подставим в (2)
х² у²· 13/(х + у) = 468
х² у²/(х + у) = 36
Получили другую систему:
(х² +у²) = 13/(х + у)
х² у² = 36 (х + у)
2) x^3 + y^3 = 1 (x + y)(x² - xy + y²) =1
x^2 y + x y^2 = 1 xy ( x + y) = 1 Разделим 1-е на 2-е. Получим:
(х² - ху + у²)/ху = 1 ⇒х² - ху + у² = ху⇒х² -2ху + у² = 0⇒(х - у)² = 0 ⇒ х = у
Сделаем эту подстановку в любое уравнение, получим
х³ + х³ = 1 ⇒2х³ = 1⇒х³ = 1/2 ⇒ х = у = ∛1/2 = ∛4/2