Пусть f(x)=ax^2+bx+c. Данные уравнения могут быть записаны в виде
ax^2+(b-5)x+(c+20)=0;\ ax^2+(b-2)x+(c+8)=0.
По условию эти уравнения имеют единственные корни, что бывает тогда и только тогда, когда их дискриминанты равны нулю, то есть
(b-5)^2-4ac-80a=0;\ (b-2)^2-4ac-32a=0.
Домножим первое выражение на 2, а второе на 5, после чего возьмем их разность:
2(b-5)^2-8ac-5(b-2)^2+20ac=0;\ 12ac=3b^2-30;\ 4ac=b^2-10,
откуда дискриминант исходного квадратного трехчлена равен
b^2-4ac=b^2-b^2+10=10.
Таким образом, дискриминант равен 10, а значит наибольшее значение, которое он может принимать, также равен 10
Мужчин - 6
Женщин - 5.
Случайным образом выбирается 3 человека. Найти вероятность что все 3 будут женского пола.
Процесс выбора 3 людей можно записать в виде цепочки последовательных действий:
Выбрали случайным образом одного человека. Выбрали случайным образом второго человека из оставшихся. Выбрали случайным образом третьего человека из оставшихся.
С данного расстолкования, можно прийти к выводу, что искомая вероятность будет найдена с правила умножения.
Первый человек женщина И второй человек тоже женщина И третий человек тоже женщина.
P(Случайным образом выбрать женщину) = 5/11
В данном случае удовлетворяют событие - 5 возможных женщин из 11 всех работников
P(Случайным образом выбрать вторую женщину из оставшихся работников) = 4/10
Одну женщину из толпы всех работников забрали, соответственно женщин осталось 4, а мужчин 6 (вместе работников 10)
P(Случайным образом выбрать третью женщину из оставшихся работников) = 3/9
Одну женщину из толпы всех работников забрали, соответственно женщин осталось 3, а мужчин 6 (вместе работников 9)
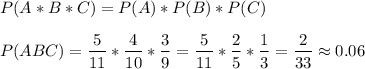
ответ: Вероятность равна 2/33 или 0,0(60)