ответ: первый насос наполнит бассейн за 10 часов .
Пусть 1 насос наполняет бассейн за х часов, тогда его производительность = 1/х (объёма бассейна в час) .
Пусть 2 насос наполняет бассейн за у часов, тогда его производительность = 1/у (объёма бассейна в час) .
Производительность 1 насоса в 1,5 раза выше производительности 2 насоса, тогда (1/х):(1/у)=1,5 ⇒ (у/х)=1,5 , у=1,5х .
Совместная производительность равна
(1/х)+(1/у)=(1/х)+(1/1,5х)=(2,5/1,5х)=5/(3х) .
Тогда за 6 часов, работая вместе, насосы наполнят 1 бассейн . ⇒
А - объём работы (1 бассейн) , р - производительность , t - время .
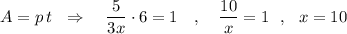
Первый насос наполнит бассейн за 10 часов, а второй за у=1,5*10=15 часов.
y = (0.25x^2 + x)x/x + 4
ОDZ: x + 4 ≠ 0 = > x ≠ – 4
1) Прямая, перпендикулярная ОХ.
2) Проходит через точку ( – 4; 0)
3) Не имеет с графиком f(x) = (0.25x^2 + x)x/x + 4 общих точек.
2.
Данные числа невозможно сравнить, потому что если bи< c, d < c, то можно сказать, что и b, и d < c и даже при этом b может быть больше d, или d ≈ больше b, или также может выполняться равенство d = b.
Поскольку a = b, то тогда тоже самое можно сказать и про число а = а может быть больше, меньше или равно d.
Тогда d и а можно сравнить только относительно с: поскольку b < c, d < c
и a = b, то и a, и d < c.