ОбъясненПлощадь трапеции равна произведению её высоты на полусумму оснований ( среднюю линию).
Обозначим трапецию АВСD, высоту - ВН. Тогда АН=4, DH=9
Высота равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности оснований, больший – их полусумме. ⇒
S=BH•HD
Треугольник АВD- прямоугольный.
Его высота – общая с высотой трапеции.
Высота прямоугольного треугольника, проведенная из прямого угла - среднее пропорциональное между отрезками, на которые она делит гипотенузу.
ВН²=АН•DH=4•9=36
BH=√36=6
S(трап)=6•9=54.
Подробнее - на -
ответ: y= -3x+11 .
Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая:  .
.
Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент k .
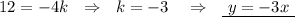
Линейная функция задаётся уравнением 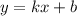 .
.
Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид 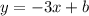
Найдём число "b" , подставив координаты точки D(7;-10) в уравнение линейной функции.
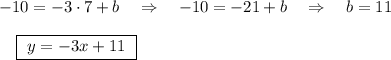
3x²-5x>0
3х²-5х- квадратичная функция график парабола ветви вверх
Д=25, х=10/6, х=0 - это точки пересечения параболы с осью Ох
3x²-5x>0 так как неравенство больше нуля, значит нас интересуют промежутки выше оси Ох
ответ:(-∞;0)U(10/6;+∞)