1.
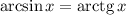
ОДЗ: арксинус определен при ![x\in[-1;\ 1]](/tpl/images/1421/5878/61ea0.png)
Найдем синус левой и правой части:
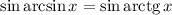
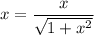
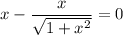
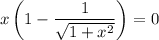
Уравнение распадается на два. Для первого уравнения получим:
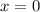
Решаем второе уравнение:
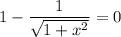
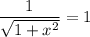
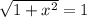
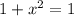
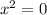
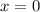
Таким образом, уравнение имеет единственный корень 0.
ответ: 0
2.
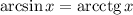
ОДЗ: арксинус определен при ![x\in[-1;\ 1]](/tpl/images/1421/5878/61ea0.png)
Найдем синус левой и правой части:
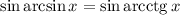
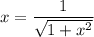
Так как в правой части стоит положительная величина, то и левая часть должна быть положительной, то есть 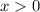 .
.
Возведем в квадрат обе части:
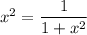
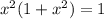
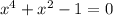
Решим биквадратное уравнение:
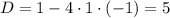
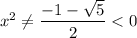
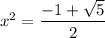
Находим х:
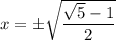
Однако, так как было выявлено ограничение 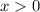 , то отрицательный корень не попадает в ответ.
, то отрицательный корень не попадает в ответ.
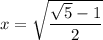
Оценив значение полученного корня, мы понимаем, что он удовлетворяет исходной ОДЗ:

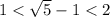
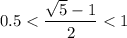
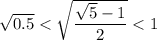
ответ: 
Я думаю, что - 2,5 или 2,5
Объяснение:
Потому что если вместо d в выражение 4d +10 подставить - 2,5, то это выражение будет равно 0,и соответственно умножаем на 0 второе выражение (4d - 10), то всё равно получится 0, и так как 0 у нас получиться в знаменателе и дробь означает знак деление то придётся делить, А НА 0 ДЕЛИТЬ НЕЛЬЗЯ, ТАК ЧТО во я объяснила свой ответ
А 2,5 мы можем подставить во второе выражение (4d - 10) и тогда и там получится 0,и тот же вывод с этим выражением
Вот так я думаю, если правильно буду очень этому рада, ну а если нет, то извини по братски
D(y) = R
Точки пересечения с осью Ох и Оу
С осью Ох
С осью Оу
(0;-5) - точки пересечения с осью Оу
Возврастание и убывание функции (точки экстремумы)
Находим производную функции
Приравниваем ее к нулю
__+___|___-___|___+___
-1 1
Функция возрастает на промежутке (-∞;-1) и (1;+∞), а убывает - (-1;1). В точке х=-1 функция имеет локальный максимум, а в точке х=-1 - локальный минимум.
Точки перегиба
Находим вторую производную
Приравниваем ее к нулю
6x =0
x=0