1. 2)
2. 3)
Объяснение:
1. 
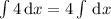, интеграл 
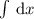табличный и равняется 
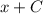, тогда исходный равняется 
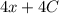, произведение констант — тоже константа, поэтому решением будет 
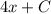, что соответствует второму варианту ответа.
2. Область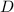 
, ограниченная указанными кривыми 
, 
, 
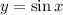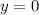и 
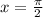, показана на приложенном рисунке. Получается, что 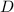задают два неравенства, 
и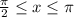 
. Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
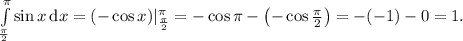
(Так получается, ибо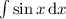 
— табличный интеграл, равный 
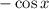, а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть 
, при известном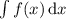 
, то есть 
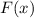, притом константа в таком случае игнорируется.)
Полученный результат соответствует третьему варианту ответа.
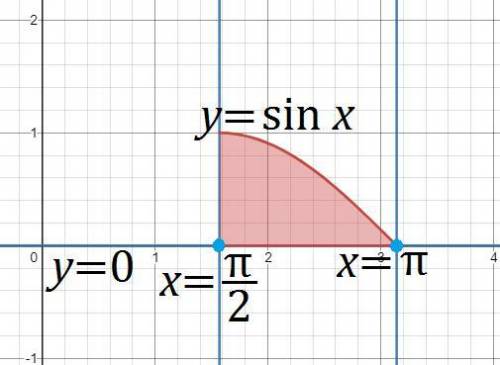
В решении.
Объяснение:
Аквалангист ныряет в морскую пучину. Известно, что через t секунд после заныривания он находится на глубине g(t) = t^2-10t.
а) Определите, на какой глубине окажется аквалангист через 4 секунды после начала ныряния.
g(t) = t²-10t = 4²-10*4 = 16-40 = -24 (м) - на этой глубине.
б) Определите, в какие моменты времени (при каких значениях t) он будет находиться на глубине 9 метров.
-9 = t²-10t
t²-10t+9=0, квадратное уравнение, ищем корни:
D=b²-4ac =100-36=64 √D= 8
х₁=(-b-√D)/2a
х₁=(10-8)/2
х₁=2/2
х₁=1 (сек.).
х₂=(-b+√D)/2a
х₂=(10+8)/2
х₂=18/2
х₂=9 (сек.)
* * * * * ура , ура , ура ааа * * * * *