Вычислите координаты точки пересечения прямых 5х-у=-25 3х+у=1

Question

Алгебра: Вычислите координаты точки пересечения прямых 5х-у=-25 3х+у=1

кам81 · Accepted Answer

Вспомним основное тригонометрическое тождество:

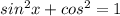$sin^{2}x+cos^{2}=1$ (на "х" внимания не обращайте, там может быть любой другой аргумент)

промежуток от пи до 3пи/2 говорит о том, что это 3 четверть на числовой окружности

В третьей четверти синус и косинус отрицательны

Следовательно наш синус тоже будет отрицательным

теперь подставим в наше тождество и выразим синус

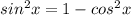
$sin^{2}x=1-cos^{2}x$

Теперь подставляем численные значения

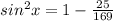
$sin^{2}x=1-\frac{25}{169}$

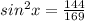
$sin^{2}x=\frac{144}{169}$

значит синус равен

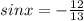
$sinx=-\frac{12}{13}$

он является отрицательным, потому что находится в 3 четверти

Итого: ваш ответ под цифрой 2

Удачи)))