Декартовы координаты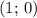 
на числовой окружности имеет угол 
.
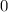Декартовы координаты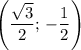 
на числовой окружности имеет угол 
.
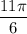Учитывая, что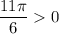 
и то, что поворот против часовой стрелки является движением в положительную сторону на числовой окружности, находим угол поворота:
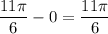
Но, так как длина одного полного оборота по числовой окружности равна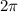 
, то, пройдя еще некоторое количество кругов в ту же сторону, мы попадем снова в исходную точку. Поэтому, все искомые углы определяются формулой:
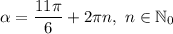, где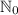 
- множество целых неотрицательных чисел
Переведем углы в градусную меру:
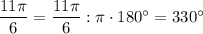
Получим новую запись:
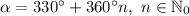
1)при пересечении графика с осью ОХ у=0 0=4х-2 4х=2 х=2:4 х=0,5
(0,5;0) т.пересечения с ОХ
при пересечении графика с осью ОУ х=0 у=4*0-2=-2
(0;-2) т.пересечения с ОУ
2) чтобы найти т.пересечения графиков надо приравнять правые части этих функций 2,8х-5=1,2х+7 и решить это уравнение
2,8х-1,2х=7+5
1,6х=12
х=12:1,6
х=7,5 подставим значение в любую функцию
у=2,8*7,5-5=21-5=16
(7,5;16) это координаты точки пересечения графиков функций y=2,8x-5 и y=1,2x+7
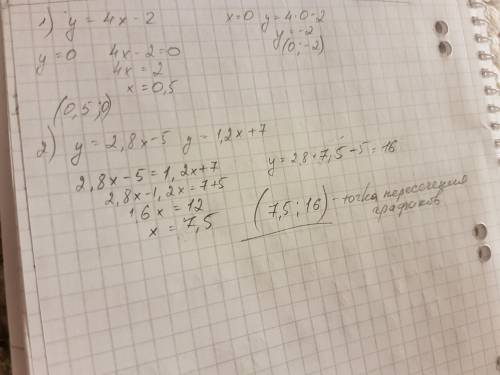
a1=x
2000=((2x+250*3)*4)/2
2000=4x+1500
4x=2000-1500
x=500/4=125
Значит самая дешевая -125 руб
An=a1+d(n-1)
A4=125+250*(4-1)=875(руб)
ответ 875 руб