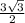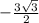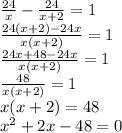
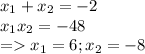Алгебра: Решить (2/x^2-4 + 1/2x-x^2): 1/x^2+4x+4=

Решить (2/x^2-4 + 1/2x-x^2): 1/x^2+4x+4=

👇

Ответ:

dhgdfnhflk

03.09.2020

$( \frac{2}{ x^{2} -4} + \frac{1}{2x- x^{2} } ): \frac{1}{ x^{2} +4x+4} =$
$( \frac{2}{(x-2)(x+2)} + \frac{x1}{x(2-x)} ): \frac{1}{(x+2)^2} =$
$(\frac{2}{(x-2)(x+2)} - \frac{1}{x(x-2)} )*(x+2^)^2=$
$\frac{2x-x-2}{x(x-2)(x+2)} *(x+2)^2= \frac{x-2}{x(x+2)(x-2)}*(x+2)^2=$
$\frac{x+2}{x}$

4,5(46 оценок)

Открыть все ответы

Ответ:

gravasamp

03.09.2020

S (км) V (км/ч) t(ч)
--------------------------------------------------------------------------------------------
1 турист 24 х +2 24/(х +2 )

2 турист 24 х 24 / х
---------------------------------------------------------------------------------------------
По условию первый турист пришел в В на 1 час раньше, чем 2 турист пришел в А, то
$\frac{24}{x} - \frac{24}{x+2} = 1 \\ 
 \frac{24(x+2) - 24x}{x(x+2)} = 1 \\ 
 \frac{24x+48 - 24x}{x(x+2)} = 1 \\ 
 \frac{48}{x(x+2)} = 1 \\ 
x(x+2) =48 \\ 
 x^{2} +2x-48=0 \\ 

$
По теореме Виета:
$x_{1} + x_{2} = -2 \\ 
 x_{1} x_{2} = - 48 \\ 
= x_{1}= 6; x_{2} = -8 \\$ (посторонний корень -8)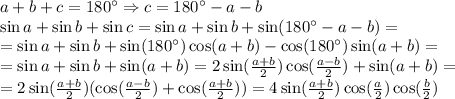
Итак скорость 2 туриста v2 = 6, тогда скорость первого v1 = 6+2 = 8.

ответ: скорости туристов 6 км/ч и 8 км/ч.

4,8(19 оценок)

Ответ:

знания2345

03.09.2020

$a+b+c=180^\circ\Rightarrow c = 180^\circ - a - b\\\sin a + \sin b + \sin c = \sin a + \sin b + \sin(180^\circ-a-b)=\\=\sin a + \sin b + \sin(180^\circ)\cos(a+b)-\cos(180^\circ)\sin(a+b)=\\=\sin a + \sin b + \sin (a + b)=2\sin({a+b\over 2})\cos({a-b\over2})+\sin(a+b)=\\=2\sin({a+b\over2})(\cos({a-b\over2})+\cos({a+b\over2}))=4\sin({a+b\over2})\cos({a\over2})\cos({b\over2})$
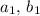Нам достаточно найти максимум при некоторых значениях $a_1,\,b_1$ , а минимум будет иметь то же по модулю значения, но обратный знак (если есть некоторое максимальное значение при 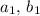$a_1,\,b_1$ , то взяв 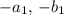$-a_1,\,-b_1$ мы получим, что синус поменяет знак на противоположный, а косинусы сохранят знак. Если же у минимума модуль больше, чем у максимума, то также поменяем знак и получим новый максимум)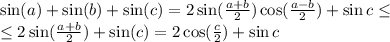
Теперь осталось найти максимум.

$\sin(a)+\sin(b)+\sin(c)=2\sin({a+b\over2})\cos({a-b\over2})+\sin c\leq\\\leq2\sin({a+b\over2})+\sin(c)=2\cos({c\over2})+\sin c$
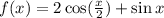Найдем наибольшее значение функции $f(x)=2\cos({x\over2})+\sin x$ :
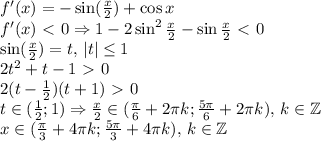
$f'(x)=-\sin({x\over2})+\cos x\\f'(x)\ \textless \ 0\Rightarrow 1-2\sin^2{x\over2}-\sin{x\over2}\ \textless \ 0\\\sin ({x\over2})=t,\,|t|\leq1\\2t^2+t-1\ \textgreater \ 0\\2(t-{1\over2})(t+1)\ \textgreater \ 0\\t\in({1\over2};1)\Rightarrow {x\over2}\in({\pi\over6}+2\pi k;{5\pi\over6}+2\pi k),\,k\in\mathbb{Z}\\x\in({\pi\over3}+4\pi k;{5\pi\over3}+4\pi k),\,k\in\mathbb{Z}$
На полученном интервале f(x) убывает. Кроме того, f(x) имеет период 4π.
Таким же образом приходим к интервалу на котором f(x) возрастает (просто меняем знак неравенства):
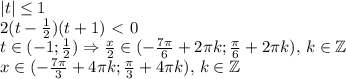
$|t|\leq1\\2(t-{1\over2})(t+1)\ \textless \ 0\\t\in(-1;{1\over2})\Rightarrow {x\over2}\in(-{7\pi\over6}+2\pi k;{\pi\over6}+2\pi k),\,k\in\mathbb{Z}\\x\in(-{7\pi\over3}+4\pi k;{\pi\over3}+4\pi k),\,k\in\mathbb{Z}$
Значит достаточно проверить значение в точках
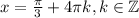
$x={\pi\over3}+4\pi k,k\in\mathbb{Z}$
Как нетрудно убедится, в этих точках
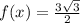
$f(x)={3\sqrt3\over2}$
Таким образом,
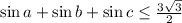
$\sin a+\sin b+\sin c\leq{3\sqrt3\over2}$
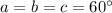Но при $a=b=c=60^\circ$ достигается это значение.

Значит максимальное значение: ${3\sqrt3\over2}$
Минимальное: $-{3\sqrt3\over2}$