5% = 0,05; 4% = 0,04
Пусть вкладчик внёс на первый счёт х грн, тогда доход по этому счёту составил 0,05х грн.
Пусть вкладчик внёс на второй счёт у грн, тогда доход по этому счёту составил 0,04у грн.
Если средства, внесённые на разные счета, поменять местами, то годовой доход по двум вкладам составит
0,04x + 0,05y = A гривен.
Составим систему
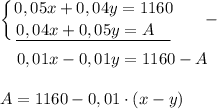
1) Если средства, внесённые на два счёта были одинаковы, то годовой доход не изменится :
x = y, x - y = 0, A = 1160
2) Если на первый счёт было внесено больше денег, чем на второй счёт, то годовой доход уменьшится :
x > y, x - y > 0, A < 1160
3) Если на первый счёт было внесено меньше денег, чем на второй счёт, то годовой доход увеличится :
x < y, x - y < 0, A > 1160
ответ : изменение годового дохода будет зависеть от количества внесённых денежных средств на разные счета.
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
а16 = 26,4 a16 = a1 + 15 d 26,4 = a1 +15d надо это систему решить
- 6,9 = -а1 - 2d
26,4 = a1 + 15 d Сложим:
19, 5 = 13 d
d = 19,5 : 13
d = 1,5